题目内容
定义域为R的奇函数f(x)满足f(x+1)=f(x-1),且当x∈(0,1)时,f(x)= .
.
(1)求f(x)在[-1,1]上的解析式;
(2)当m取何值时,方程f(x)=m在(0,1)上有解?
解析:(1)当x∈(-1,0)时,-x∈(0,1),由f(x)为R上的奇函数,得f(x)=-f(-x)=- =
= ,x∈(-1,0),且f(0)=0,因为f(x)满足f(x+1)=f(x-1),所以f(1)=-f(-1)=-f(1),所以f(1)=f(-1)=0,
,x∈(-1,0),且f(0)=0,因为f(x)满足f(x+1)=f(x-1),所以f(1)=-f(-1)=-f(1),所以f(1)=f(-1)=0,
 所以f(x)=
所以f(x)=
(2)当x∈(0,1),m= =1-
=1- ,2x∈(1,2),2x+1∈(2,3),所以
,2x∈(1,2),2x+1∈(2,3),所以 ∈
∈ ,所以1-
,所以1- ∈
∈ ,即m∈
,即m∈ .
.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
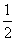 ,f2(x)=x-1,f3(x)=x2,求f1(f2(f3(2 012)))的值.
,f2(x)=x-1,f3(x)=x2,求f1(f2(f3(2 012)))的值. ,曲线y=f(x)在点(2,f(2))处的切线方程为7x-4y-12=0.
,曲线y=f(x)在点(2,f(2))处的切线方程为7x-4y-12=0. 直线x=0和直线y=x所围成的三角形面积为定值,并求此定值.
直线x=0和直线y=x所围成的三角形面积为定值,并求此定值. B.f(x)≤f(1)
B.f(x)≤f(1) 时,讨论f(x)的单调
时,讨论f(x)的单调
 数f(x)=
数f(x)= 则f(f(-1))=( )
则f(f(-1))=( ) D.2
D.2