题目内容
(本小题满分12分)
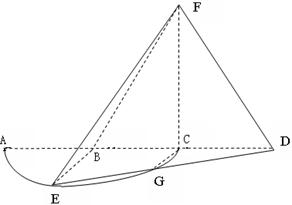
如图,四棱锥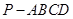 的底面是正方形,
的底面是正方形,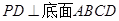 ,点E在棱PB上.
,点E在棱PB上.
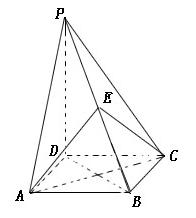
(Ⅰ)求证:PB⊥AC;
(Ⅱ) 当PD=2AB,E在何位置时, PB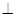 平面EAC;
平面EAC;
(Ⅲ) 在(Ⅰ)的情况下,求二面E-AC-B的余弦值.
如图,四棱锥
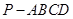 的底面是正方形,
的底面是正方形,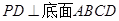 ,点E在棱PB上.
,点E在棱PB上.
(Ⅰ)求证:PB⊥AC;
(Ⅱ) 当PD=2AB,E在何位置时, PB
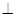 平面EAC;
平面EAC;(Ⅲ) 在(Ⅰ)的情况下,求二面E-AC-B的余弦值.
(Ⅰ)见解析;(Ⅱ) ,PB
,PB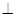 平面EAC;
平面EAC;
(Ⅲ)二面角E-AC-B的余弦值为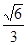 .
.
 ,PB
,PB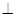 平面EAC;
平面EAC;(Ⅲ)二面角E-AC-B的余弦值为
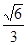 .
.本试题主要是考查了线线垂直的判定和线面垂直求解以及二面角的平面角的综合运用。
(1)以D为原点DA、DC、DZ分别为x轴、y轴、z轴建立空间直角坐标系,求解点的坐标,进而求解向量的坐标,得到垂直关系的证明。
(2)利用直线的方向向量与平面的法向量来分析如果平行,则说明线面垂直。
(3)借助于平面的法向量与法向量的夹角来表示二面角的平面角的大小。
解 以D为原点DA、DC、DZ分别为x轴、y轴、z轴建立空间直角坐标系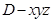 设
设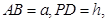
则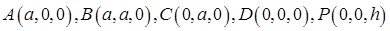 ,
,
(Ⅰ)∵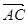 =
=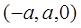 ,
,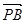 =
=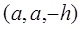
∴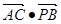 =
=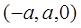
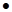
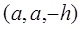 =0
=0
∴AC⊥PC
(Ⅱ)当PD=2AB时,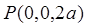 ,
,
由(Ⅰ)知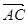 ⊥
⊥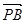 ,故只要
,故只要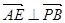 即可
即可
设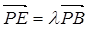 ,
,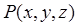 ,则
,则
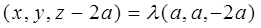 ,∴
,∴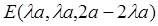
∴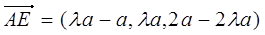
由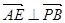 得
得
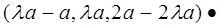
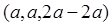 =0
=0
∴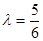
所以 ,PB
,PB 平面EAC;
平面EAC;
(Ⅲ)由(Ⅱ)知 ,设
,设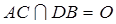 ,则
,则
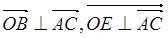 ,
, 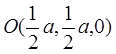
∴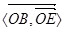 等于二面E-AC-B的平面角
等于二面E-AC-B的平面角
∴ ,
,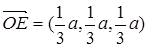
∴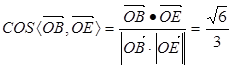
∴二面角E-AC-B的余弦值为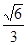
(1)以D为原点DA、DC、DZ分别为x轴、y轴、z轴建立空间直角坐标系,求解点的坐标,进而求解向量的坐标,得到垂直关系的证明。
(2)利用直线的方向向量与平面的法向量来分析如果平行,则说明线面垂直。
(3)借助于平面的法向量与法向量的夹角来表示二面角的平面角的大小。
解 以D为原点DA、DC、DZ分别为x轴、y轴、z轴建立空间直角坐标系
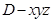 设
设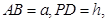
则
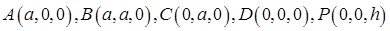 ,
,(Ⅰ)∵
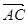 =
=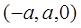 ,
,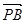 =
=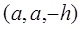
∴
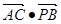 =
=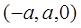
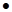
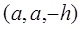 =0
=0∴AC⊥PC
(Ⅱ)当PD=2AB时,
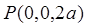 ,
,
由(Ⅰ)知
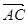 ⊥
⊥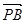 ,故只要
,故只要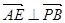 即可
即可设
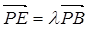 ,
,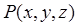 ,则
,则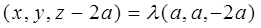 ,∴
,∴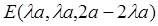
∴
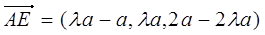
由
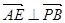 得
得
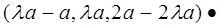
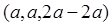 =0
=0∴
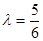
所以
 ,PB
,PB 平面EAC;
平面EAC;(Ⅲ)由(Ⅱ)知
 ,设
,设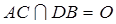 ,则
,则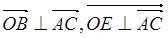 ,
, 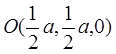
∴
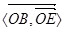 等于二面E-AC-B的平面角
等于二面E-AC-B的平面角 ∴
 ,
,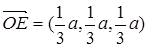
∴
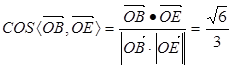
∴二面角E-AC-B的余弦值为
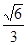

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
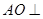 平面BCD;
平面BCD;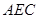 是半径为
是半径为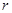 的半圆,
的半圆,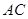 为直径,点
为直径,点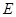 为弧
为弧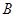 和点
和点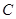 为线段
为线段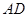 的三等分点,线段
的三等分点,线段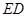 与弧
与弧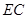 交于点
交于点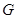 ,且
,且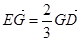 ,平面
,平面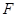 满足
满足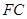
 平面
平面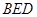 ,
,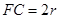 。
。
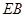
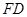 ;
; (及其内部)绕
(及其内部)绕 是空间三条直线,
是空间三条直线, 是空间两个平面,则下列命题中,逆命题不正确的是( )
是空间两个平面,则下列命题中,逆命题不正确的是( ) 时,若
时,若 ,则
,则
 时,若
时,若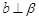 ,则
,则
 且
且 是
是 在
在 内的射影时,若
内的射影时,若 ,则
,则
 时,若
时,若 ,则
,则
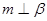 .(填所选条件的序号)
.(填所选条件的序号) 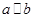 ,a与c的夹角为
,a与c的夹角为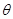 ,那么b与c的夹角为( )
,那么b与c的夹角为( ) ,
,
 ,则二面角
,则二面角 的大小( )
的大小( )
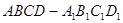 中,
中,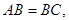
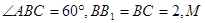 为
为 中点,点
中点,点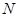 在
在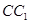 上。(1)试确定点
上。(1)试确定点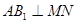 ;(2)当
;(2)当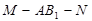 的正切值。
的正切值。