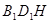题目内容
(本题满分12分,每一问6分)
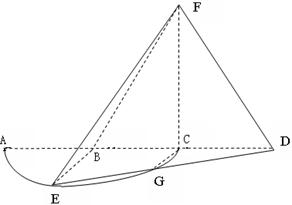
如图,弧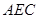 是半径为
是半径为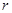 的半圆,
的半圆,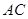 为直径,点
为直径,点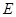 为弧
为弧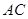 的中点,点
的中点,点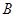 和点
和点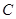 为线段
为线段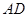 的三等分点,线段
的三等分点,线段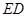 与弧
与弧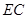 交于点
交于点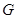 ,且
,且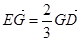 ,平面
,平面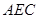 外一点
外一点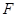 满足
满足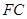
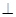 平面
平面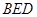 ,
,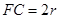 。
。
⑴证明: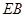
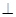
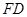 ;
;
⑵ 将 (及其内部)绕
(及其内部)绕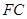 所在直线旋转一周形成一几何体,求该几何体的体积。
所在直线旋转一周形成一几何体,求该几何体的体积。
如图,弧
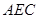 是半径为
是半径为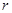 的半圆,
的半圆,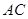 为直径,点
为直径,点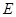 为弧
为弧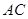 的中点,点
的中点,点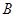 和点
和点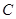 为线段
为线段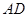 的三等分点,线段
的三等分点,线段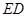 与弧
与弧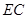 交于点
交于点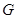 ,且
,且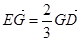 ,平面
,平面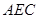 外一点
外一点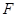 满足
满足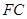
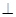 平面
平面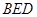 ,
,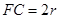 。
。
⑴证明:
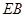
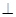
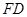 ;
;⑵ 将
 (及其内部)绕
(及其内部)绕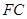 所在直线旋转一周形成一几何体,求该几何体的体积。
所在直线旋转一周形成一几何体,求该几何体的体积。⑴ 证明: 见解析;⑵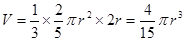 。
。
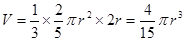 。
。本试题主要是考查了圆内几何性质,以及线面垂直的判定定理,以及关于圆锥的体积的运算的综合运用。
(1)由于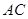 为直径,点
为直径,点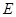 为弧
为弧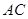 的中点,
的中点,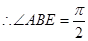 ,即
,即 又
又
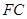
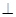 平面
平面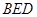 ,
, 平面
平面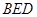 ,
, ,进而得到线面垂直,利用性质定理得到线线垂直的证明。
,进而得到线面垂直,利用性质定理得到线线垂直的证明。
(2)建立空间直角坐标系,则相关点的坐标为 ,
,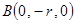 ,
,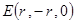 ,
,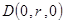 ,利用两点的距离公式得到高的长度,然后求解椎体的体积公式即可。
,利用两点的距离公式得到高的长度,然后求解椎体的体积公式即可。
⑴ 证明: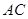 为直径,点
为直径,点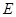 为弧
为弧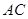 的中点,
的中点,
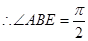 ,即
,即 。………2分
。………2分
又
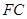
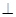 平面
平面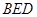 ,
, 平面
平面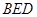 ,
,
 ,
,
 由
由 平面
平面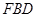 ,……4分
,……4分
又
 平面
平面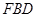 ,
,

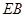
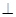
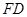 。…………………………………………………………………………6分
。…………………………………………………………………………6分
⑵ 如图所示,建立空间直角坐标系,则相关点的坐标为 ,
,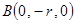 ,
,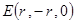 ,
,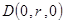 ,……………………………………7分
,……………………………………7分
设 则由
则由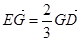 ,得
,得
 ,……………………………………………………………………9分
,……………………………………………………………………9分
则 ,由题设知,所得几何体为圆锥,其底面积为
,由题设知,所得几何体为圆锥,其底面积为 ,高为
,高为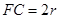 。…………………………………………………11分
。…………………………………………………11分
所以该圆锥的体积为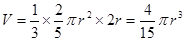 。………………………………12分
。………………………………12分
(1)由于
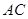 为直径,点
为直径,点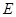 为弧
为弧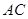 的中点,
的中点,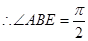 ,即
,即 又
又
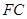
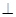 平面
平面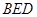 ,
, 平面
平面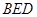 ,
, ,进而得到线面垂直,利用性质定理得到线线垂直的证明。
,进而得到线面垂直,利用性质定理得到线线垂直的证明。(2)建立空间直角坐标系,则相关点的坐标为
 ,
,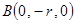 ,
,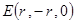 ,
,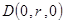 ,利用两点的距离公式得到高的长度,然后求解椎体的体积公式即可。
,利用两点的距离公式得到高的长度,然后求解椎体的体积公式即可。⑴ 证明:
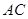 为直径,点
为直径,点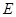 为弧
为弧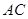 的中点,
的中点,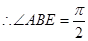 ,即
,即 。………2分
。………2分又

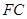
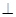 平面
平面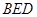 ,
, 平面
平面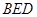 ,
, ,
, 由
由 平面
平面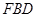 ,……4分
,……4分又

 平面
平面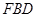 ,
,
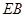
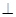
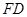 。…………………………………………………………………………6分
。…………………………………………………………………………6分⑵ 如图所示,建立空间直角坐标系,则相关点的坐标为
 ,
,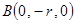 ,
,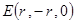 ,
,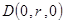 ,……………………………………7分
,……………………………………7分设
 则由
则由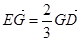 ,得
,得
 ,……………………………………………………………………9分
,……………………………………………………………………9分则
 ,由题设知,所得几何体为圆锥,其底面积为
,由题设知,所得几何体为圆锥,其底面积为 ,高为
,高为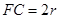 。…………………………………………………11分
。…………………………………………………11分所以该圆锥的体积为
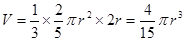 。………………………………12分
。………………………………12分
练习册系列答案
相关题目
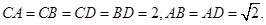
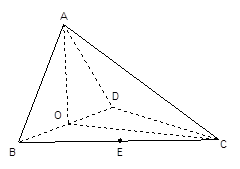
 平面BCD;
平面BCD;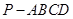 的底面是正方形,
的底面是正方形,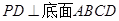 ,点E在棱PB上.
,点E在棱PB上.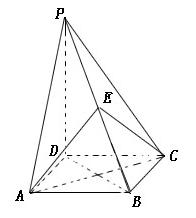
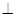 平面EAC;
平面EAC;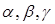 是三个不同的平面,给出下列四个命题:
是三个不同的平面,给出下列四个命题: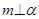 ,
,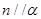 ,则
,则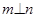 ②若
②若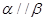 ,
,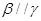 ,
,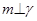
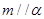 ,
,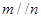 ④若
④若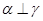 ,
,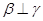 ,则
,则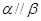
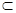 α,则α∥β;
α,则α∥β;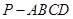 为正四棱锥,几何体
为正四棱锥,几何体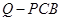 为正四面体.、
为正四面体.、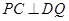 ;
;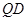 与平面
与平面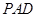 所成角的正弦值.
所成角的正弦值.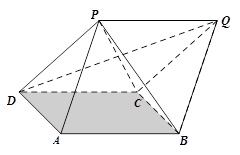
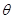 角的直线一定有无穷多条
角的直线一定有无穷多条 、
、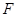 、
、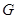 、
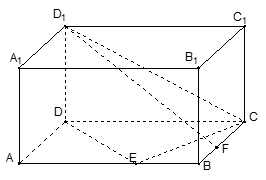
、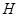 分别是正方体
分别是正方体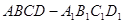 的棱
的棱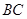 、
、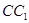 、
、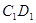 、
、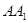 的中点。
的中点。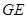 ∥平面
∥平面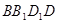 ;
;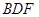 ∥平面
∥平面