题目内容
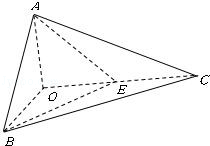
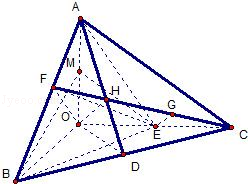
已知三棱锥O﹣ABC的侧棱OA,OB,OC两两垂直,且OA=1,OB=OC=2,E是OC的中点.
(1)求O点到面ABC的距离;
(2)求异面直线BE与AC所成的角;
(3)求二面角E﹣AB﹣C的大小.
(1)求O点到面ABC的距离;
(2)求异面直线BE与AC所成的角;
(3)求二面角E﹣AB﹣C的大小.
解:(1)取BC的中点D,连AD、OD
因为OB=OC,则OD⊥BC、AD⊥BC, ∴BC⊥面OAD.
过O点作OH⊥AD于H,
则OH⊥面ABC,OH的长就是所求的距离 .
又BC=2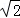 ,OD=
,OD=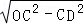 =
=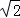 ,
,
又OA⊥OB,OA⊥OC
∴OA⊥面OBC,则OA⊥OD
AD =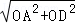 =
=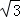 ,
,
在直角三角形OAD中,有OH=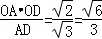
(2)取OA的中点M,连EM、BM,
则EM∥AC,DBEM是异面直线BE与AC所成的角,
易求得EM=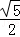 ,BE=
,BE=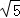 ,BM=
,BM=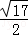 .
.
由余弦定理可求得cos∠BEM=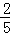 ,
,
∴∠BEM=arccos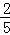
(3)连CH并延长交AB于F,连OF、EF.
由OC⊥面OAB,得OC⊥AB,
又OH⊥面ABC,所以CF⊥AB,EF⊥AB,
则DEFC就是所求的二面角的平面角.
作EG⊥CF于G,则EG= OH=
OH= 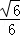 ,
,
在Rt△OAB中,OF=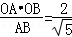
在Rt△OEF中,EF=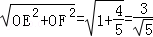
∴sin∠EFG=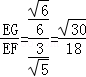
∴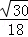 ∠EFG=arcsin
∠EFG=arcsin 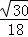 .
.
因为OB=OC,则OD⊥BC、AD⊥BC, ∴BC⊥面OAD.
过O点作OH⊥AD于H,
则OH⊥面ABC,OH的长就是所求的距离 .
又BC=2
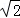 ,OD=
,OD=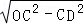 =
=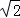 ,
,又OA⊥OB,OA⊥OC
∴OA⊥面OBC,则OA⊥OD
AD =
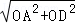 =
=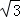 ,
,在直角三角形OAD中,有OH=
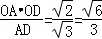
(2)取OA的中点M,连EM、BM,
则EM∥AC,DBEM是异面直线BE与AC所成的角,
易求得EM=
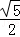 ,BE=
,BE=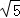 ,BM=
,BM=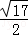 .
.由余弦定理可求得cos∠BEM=
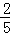 ,
,∴∠BEM=arccos
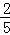
(3)连CH并延长交AB于F,连OF、EF.
由OC⊥面OAB,得OC⊥AB,
又OH⊥面ABC,所以CF⊥AB,EF⊥AB,
则DEFC就是所求的二面角的平面角.
作EG⊥CF于G,则EG=
 OH=
OH= 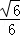 ,
,在Rt△OAB中,OF=
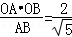
在Rt△OEF中,EF=
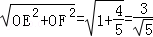
∴sin∠EFG=
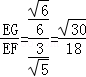
∴
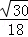 ∠EFG=arcsin
∠EFG=arcsin 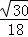 .
. 

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案
相关题目
 如图,已知三棱锥O-ABC的侧棱OA,OB,OC两两垂直,且OA=1,OB=OC=2,E是OC的中点.
如图,已知三棱锥O-ABC的侧棱OA,OB,OC两两垂直,且OA=1,OB=OC=2,E是OC的中点. 如图,已知三棱锥O-ABC的侧棱OA,OB,OC两两垂直,且OA=1,OB=OC=2,D是BC的中点,E是OC的中点.
如图,已知三棱锥O-ABC的侧棱OA,OB,OC两两垂直,且OA=1,OB=OC=2,D是BC的中点,E是OC的中点. (2012•月湖区模拟)已知三棱锥O-ABC,OA、OB、OC两两垂直且长度均为6,长为2的线段MN的一个端点M在棱OA上运动,另一个端点N在△OBC内运动(含边界),则MN的中点P的轨迹与三棱锥的面OAB、OBC、OAC围成的几何体的体积为
(2012•月湖区模拟)已知三棱锥O-ABC,OA、OB、OC两两垂直且长度均为6,长为2的线段MN的一个端点M在棱OA上运动,另一个端点N在△OBC内运动(含边界),则MN的中点P的轨迹与三棱锥的面OAB、OBC、OAC围成的几何体的体积为