题目内容
18.已知函数f(x)是偶函数,且f(x-2)在[0,2]上是减函数,则( )| A. | f(0)<f(-1)<f(2) | B. | f(-1)<f(0)<f(2) | C. | f(-1)<f(2)<f(0) | D. | f(2)<f(0)<f(-1) |
分析 根据函数奇偶性和单调性的关系,进行转化求解即可.
解答 解:∵f(x)是偶函数,且f(x-2)在[0,2]上是减函数,
∴f(x)在[-2,0]上是减函数,
则f(x)在[0,2]上是增函数,
则f(0)<f(1)<f(2),即f(0)<f(-1)<f(2),
故选:A
点评 本题主要考查函数值的大小比较,根据函数奇偶性和单调性的关系进行转化是解决本题的关键.

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
6.已知函数f(x)=lg(ax-bx),(a,b为常数,a>1>b>0),若x∈(2,+∞)时,f(x)>0恒成立,则( )
| A. | a2-b2>1 | B. | a2-b2≥1 | C. | a2-b2<1 | D. | a2-b2≤1 |
13.在面积为1的等边三角形ABC内任取一点,使三角形△ABP,△ACP,△BCP的面积都小于$\frac{1}{2}$的概率为( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
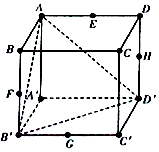 已知立方体ABCD-A'B'C'D',E,F,G,H分别是棱AD,BB',B'C',DD'中点,从中任取两点确定的直线中,与平面AB'D'平行的有( )条.
已知立方体ABCD-A'B'C'D',E,F,G,H分别是棱AD,BB',B'C',DD'中点,从中任取两点确定的直线中,与平面AB'D'平行的有( )条.