题目内容
设二次函数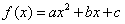 (
(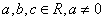 )满足条件:
)满足条件:
(1)当 时,
时,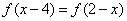 ,且
,且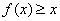 ;
;
(2)当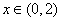 时,
时,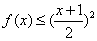 ;
;
(3)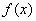 在R上的最小值为0,求最大的
在R上的最小值为0,求最大的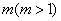 ,使得存在
,使得存在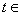 R,只要
R,只要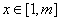 ,就有
,就有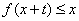 .
.
由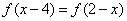 ,
, ,可知二次函数
,可知二次函数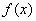 的对称轴为直线
的对称轴为直线 ,
,
又由(3)知,二次函数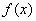 的开口向上,即
的开口向上,即 ,设
,设 (
( ).
).
由(1)知 ,由(2)知
,由(2)知 ,所以
,所以 .
.
即 ,所以
,所以 ,即
,即 .
.
因为 的图象开口向上,而
的图象开口向上,而 的图象是由
的图象是由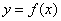 的图象向左平移
的图象向左平移 个单位得到.要在区间
个单位得到.要在区间 上,使得
上,使得 的图象在
的图象在 的图象的下方,且
的图象的下方,且 最大,则1和
最大,则1和 应当是关于
应当是关于 的方程
的方程  ①的两个根.
①的两个根.
令 代入方程①,得
代入方程①,得 或
或 .
.
 当
当 时,方程①的解为
时,方程①的解为 ,这与
,这与 矛盾.
矛盾.
当 时,方程①的解为
时,方程①的解为 ,所以
,所以
 .又当
.又当 时,对任意
时,对任意 ,恒有
,恒有 ,即
,即 ,也就是
,也就是 ,所以
,所以 的最大值为9.
的最大值为9.

练习册系列答案
相关题目
某服装加工厂某月生产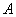 、
、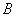 、
、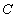 三种产品共4000件,为了保证产品质量,进行抽样检验,根据分层抽样的结果,企业统计员制作了如下的统计表格:
三种产品共4000件,为了保证产品质量,进行抽样检验,根据分层抽样的结果,企业统计员制作了如下的统计表格:
| 产品类别 |
|
|
|
| 产品数量(件) |
| ||
| 样本容量(件) | 230 |
由 于不小心,表格中
于不小心,表格中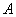 、
、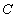 产品的有关数据已被污染看不清楚,统计员记得
产品的有关数据已被污染看不清楚,统计员记得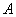 产品
产品 的样本容量
的样本容量 比
比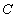 产品的样本容量多
产品的样本容量多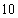 ,根据以上信息,可得
,根据以上信息,可得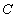 的产品数量是________.
的产品数量是________.
 _对.
_对.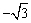 ,0),F(
,0),F(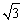 ,0),圆F:
,0),圆F: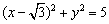 .动点P满足PE+PF=4.以P为圆心,OP为半径的圆P与圆F的一个公共点为Q.
.动点P满足PE+PF=4.以P为圆心,OP为半径的圆P与圆F的一个公共点为Q.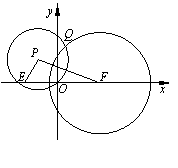
 ,区间
,区间 ,集合
,集合 ,则使
,则使 成立的实数对(a,b)有 对?
成立的实数对(a,b)有 对? ,使
,使 上的值域为
上的值域为 ,那么
,那么 是对称函数,则
是对称函数,则 的取值范围是 .
的取值范围是 . 或
或 ; (2)
; (2)  或
或 ; (3)
; (3)  且
且 ; (4)
; (4)  .
. 2300
2300 是椭圆
是椭圆 的两个焦点,
的两个焦点, 在椭圆上,且
在椭圆上,且 ,则
,则 的面积是 .
的面积是 .