题目内容
14.在△ABC中,点D在边CB的延长线上,且$\overrightarrow{CD}$=4$\overrightarrow{BD}$=r$\overrightarrow{AB}$-s$\overrightarrow{AC}$,r,s∈R,求s+r的值.分析 可画出图形,根据条件便有$\overrightarrow{CD}=\frac{4}{3}\overrightarrow{CB}=\frac{4}{3}\overrightarrow{AB}-\frac{4}{3}\overrightarrow{AC}$,从而便可根据平面向量基本定理得到$r=s=\frac{4}{3}$,这样便可求出s+r的值.
解答 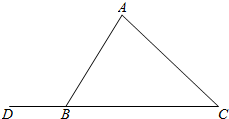 解:如图,
解:如图,
$\overrightarrow{CD}=4\overrightarrow{BD}$;
∴$\overrightarrow{CD}=\frac{4}{3}\overrightarrow{CB}=\frac{4}{3}(\overrightarrow{AB}-\overrightarrow{AC})$=$\frac{4}{3}\overrightarrow{AB}-\frac{4}{3}\overrightarrow{AC}$;
又$\overrightarrow{CD}=r\overrightarrow{AB}-s\overrightarrow{AC}$;
∴$\left\{\begin{array}{l}{r=\frac{4}{3}}\\{s=\frac{4}{3}}\end{array}\right.$;
∴$s+r=\frac{8}{3}$.
点评 考查向量数乘及向量减法的几何意义,以及向量的数乘运算,平面向量基本定理.

练习册系列答案
相关题目
4.已知$f(x)=\frac{{\sqrt{1-{x^2}}}}{2x}$,则函数f(x)的定义域为( )
| A. | [-1,1] | B. | (-1,1) | C. | (-1,0)∪(0,1) | D. | [-1,0)∪(0,1] |
6.下列各函数中,在(0,+∞)内为增函数的是( )
| A. | y=-2x+1 | B. | y=-x2 | C. | y=x-2 | D. | y=2x2 |
3.已知数列f(x)=x4+(2-a)x2+x2(lnx)2+1,x>0,若f(x)≥0恒成立,则实数a的取值范围是( )
| A. | (-∞,2] | B. | (-∞,4] | C. | [2,+∞) | D. | [4,+∞) |
4.已知函数f(x)若f(x)=$\left\{\begin{array}{l}{{2}^{x}(x≤0)}\\{{x}^{2}-2x+1(x>0)}\end{array}\right.$,g(x)=f(x)-k有3个零点,则实数k的取值范围是( )
| A. | (1,+∞) | B. | (0,1)∪(1,+∞) | C. | (0,1) | D. | (0,1] |