题目内容
在棱长为
的正方体
中，错误的是（ ）
A．直线 和直线 所成角的大小为 |
B．直线 平面 |
C．二面角 的大小是 |
D．直线 到平面 的距离为 |
D
解析试题分析：根据题意，在棱长为的正方体中，由于异面直线所成的角，按照平移法得到直线和直线所成角的大小为成立，对于线线平行，得到线面平行可知，直线
得到平面成立。对于二面角的大小是利用定义法可知得到成立，故排除法选D.
考点：命题的真假
点评：主要是考查了空间中线面位置关系的运用，属于基础题。
练习册系列答案
相关题目
设
，
是两条不同的直线，
是一个平面，则下列命题正确的是 （ ）
A．若 ， ，则 | B．若， ，则 |
C． ，，则 | D．若， ，则 |
三棱柱
中，
与
、
所成角均为
，
，且
，则三棱锥
的体积为（ ）
A． | B． | C． | D． |
已知三棱锥S-ABC，G1，G2分别为△SAB，△SAC的重心，则G1G2与△SBC，△ABC所在平面的位置关系是 ( )
| A．垂直和平行 | B．均为平行 | C．均为垂直 | D．不确定 |
正方体的棱长为1，
、
、
分别为三条棱的中点，
、
是顶点，那么点到截面
的距离是( )
A． | B． |
C． | D． |
关于直线a,b,c以及平面M，N，给出下面命题：
①若a//M，b//M, 则a//b ②若a//M, b⊥M，则b⊥a
③若a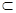
M，b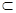M,且c⊥a，c⊥b,则c⊥M ④若a⊥M, a//N，则M⊥N
其中正确的命题是
| A．①② | B．②③ | C．②④ | D．①④ |
设
、
是两个不同的平面，
是一条直线，以下命题中，正确的是（ ）
A．若 ， ，则 | B．若 ，  ，则 |
C．若，，则 | D．若，，则 |
如图，已知长方体
中， 
,
,则二面角
的余弦值为
A． | B． | C． | D． |
设
是两条不同的直线,
是两个不同的平面,下列命题中正确的是( )
A．若 , , ,则 |
B．若 ,,,则 |
| C．若,,,则 |
D．若 ,, ,则 |