题目内容
8.某做酱菜的师傅通常用半径为1米的扇形铁皮制成一个圆锥形的盖,用来盖酱菜缸,则酱菜缸盖的最大体积为$\frac{2\sqrt{3}π}{27}$.分析 设圆锥底面半径为r,用r表示出圆锥的高,得出体积关于r的函数,利用导数求出此函数的最大值.
解答 解:设酱菜缸盖的底面半径为r,则酱菜缸盖的盖为h=$\sqrt{1-{r}^{2}}$.(0<r<1).
∴酱菜缸盖的体积V=$\frac{1}{3}π{r}^{2}h$=$\frac{1}{3}π{r}^{2}\sqrt{1-{r}^{2}}$=$\frac{1}{3}π$$\sqrt{{r}^{4}-{r}^{6}}$.
令f(r)=r4-r6,则f′(r)=4r3-6r5.
令f′(r)=0解得r=$\frac{\sqrt{6}}{3}$.
当0$<r<\frac{\sqrt{6}}{3}$时,f′(r)>0,当$\frac{\sqrt{6}}{3}<r<1$时,f′(r)<0.
∴当r=$\frac{\sqrt{6}}{3}$时,f(r)取得最大值f($\frac{\sqrt{6}}{3}$)=$\frac{4}{27}$.
∴V的最大值为$\frac{1}{3}π×\sqrt{\frac{4}{27}}$=$\frac{2\sqrt{3}π}{27}$.
故答案为:$\frac{2\sqrt{3}π}{27}$.
点评 本题考查了圆锥的结构特征,函数的最值,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.将函敬y=sin2x的图象向右平移$\frac{π}{4}$个单位长度,所得图象对应的函数解析式是( )
| A. | y=cos2x | B. | y=-cos2x | C. | y=sin(2x-$\frac{π}{4}$) | D. | y=-sin2x |
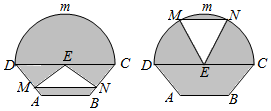 如图所示的是自动通风设施.该设施的下部ABCD是等腰梯形,其中AB=1米,高0.5米,CD=2米.上部CmD是个半圆,固定点E为CD的中点.△EMN是由电脑控制其形状变化的三角通风窗(阴影部分均不通风),MN是可以沿设施边框上下滑动且始终保持和CD平行的伸缩横杆.
如图所示的是自动通风设施.该设施的下部ABCD是等腰梯形,其中AB=1米,高0.5米,CD=2米.上部CmD是个半圆,固定点E为CD的中点.△EMN是由电脑控制其形状变化的三角通风窗(阴影部分均不通风),MN是可以沿设施边框上下滑动且始终保持和CD平行的伸缩横杆.