题目内容
某高校“统计初步”课程教师随机调查了选该课的一些学生情况,共调查了50个人,其中女生27人,男生23人.女生中有20人选统计专业,另外7人选非统计专业;男生中中有10人统计专业,另外,13人选非统计专业.求:
(1)根据以上数据完成下列的2×2列联表;
(2)根据以上数据,我们有多少的把握认为主修统计专业与性别有关系?
参考:x2=
(1)根据以上数据完成下列的2×2列联表;
(2)根据以上数据,我们有多少的把握认为主修统计专业与性别有关系?
| P(x2≥k) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| k | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| 专业 性别 |
非统计专业 | 统计专业 | 总计 |
| 男 | |||
| 女 | |||
| 总计 | 50 |
考点:独立性检验
专题:阅读型
分析:(1)根据题意填空可得列联表;
(2)利用公式计算相关指数K2的观测值,比较与临界值的大小可得判断主修统计专业与性别有关的可靠性程度.
(2)利用公式计算相关指数K2的观测值,比较与临界值的大小可得判断主修统计专业与性别有关的可靠性程度.
解答:
解:(1)2×2列联表为:
(2)K2=
=4.844>3.845,
∴有95%的把握认为主修统计专业与性别有关.
| 专业 性别 |
非统计专业 | 统计专业 | 总计 |
| 男 | 13 | 10 | 23 |
| 女 | 7 | 20 | 27 |
| 总计 | 20 | 30 | 50 |
| 50×(13×20-7×10)2 |
| 20×30×23×27 |
∴有95%的把握认为主修统计专业与性别有关.
点评:本题考查了独立性检验思想方法,根据公式计算相关指数K2的观测值是解题的关键.

练习册系列答案
相关题目
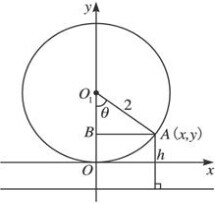 如图,某大风车的半径为2米,每12秒旋转一周,它的最低点O离地面0.5米.风车圆周上一点A从最低点O开始,运动t秒后与地面的距离为h米.以O为原点,过点O的圆的切线为x轴,建立直角坐标系.
如图,某大风车的半径为2米,每12秒旋转一周,它的最低点O离地面0.5米.风车圆周上一点A从最低点O开始,运动t秒后与地面的距离为h米.以O为原点,过点O的圆的切线为x轴,建立直角坐标系.