题目内容
10.已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$的左焦点F为圆x2+y2+2x=0的圆心,且椭圆上的点到点F的距离的最小值为$\sqrt{2}-1$.(1)求椭圆的方程;
(2)已知经过点F的动直线l与椭圆交于不同的两点A,B,点$M({-\frac{5}{4},0})$,求$\overrightarrow{MA}•\overrightarrow{MB}$的值.
分析 (1)先求出圆心坐标,再根据题意求出a、b,得椭圆的标准方程.
(2)根据直线的斜率是否存在,分情况设直线方程,再与椭圆方程联立方程组,设出交点坐标,结合韦达定理根与系数的关系,利用向量坐标运算验证.
解答 解:(1)∵圆x2+y2+2x=0的圆心为(-1,0),
依据题意c=1,a-c=$\sqrt{2}$-1,
∴a=$\sqrt{2}$,b=$\sqrt{{a}^{2}-{c}^{2}}$=1,
∴椭圆的标准方程是:$\frac{{x}^{2}}{2}$+y2=1;
(2)①当直线l与x轴垂直时,l的方程是:x=-1,
得A(-1,$\frac{\sqrt{2}}{2}$),B(-1,-$\frac{\sqrt{2}}{2}$),
$\overrightarrow{MA}$•$\overrightarrow{MB}$=($\frac{1}{4}$,$\frac{\sqrt{2}}{2}$)•($\frac{1}{4}$,-$\frac{\sqrt{2}}{2}$)=$\frac{1}{16}$-$\frac{1}{2}$=-$\frac{7}{16}$;
②当直线l与x轴不垂直时,设直线l的方程为 y=k(x+1),
代入椭圆方程,可得(1+2k2)x2+4k2x+2k2-2=0,
设A(x1,y1),B(x2,y2),
则x1x2=$\frac{2{k}^{2}-2}{1+2{k}^{2}}$,x1+x2=-$\frac{4{k}^{2}}{1+2{k}^{2}}$,
$\overrightarrow{MA}$•$\overrightarrow{MB}$=(x1+$\frac{5}{4}$,y1)•(x2+$\frac{5}{4}$,y2)
=x1x2+$\frac{5}{4}$(x1+x2)+$\frac{25}{16}$+k2(x1x2+x1+x2+1)
=(1+k2)x1x2+(k2+$\frac{5}{4}$)(x1+x2)+k2+$\frac{25}{16}$
=(1+k2)($\frac{2{k}^{2}-2}{1+2{k}^{2}}$)+(k2+$\frac{5}{4}$)(-$\frac{4{k}^{2}}{1+2{k}^{2}}$)+k2+$\frac{25}{16}$
=$\frac{-4{k}^{2}-2}{1+2{k}^{2}}$+$\frac{25}{16}$=-2+$\frac{25}{16}$=-$\frac{7}{16}$
综上$\overrightarrow{MA}$•$\overrightarrow{MB}$=-$\frac{7}{16}$.
点评 本题考查直线与圆锥曲线的综合问题及向量坐标运算.根据韦达定理,巧妙利用根与系数的关系设而不求,是解决本类问题的关键.

 名校课堂系列答案
名校课堂系列答案| A. | 钝角三角形 | B. | 直角三角形 | ||
| C. | 锐角三角形 | D. | 由增加的长度决定 |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 4 |
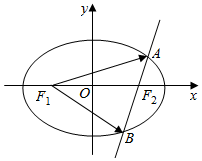 已知椭圆C的中心在原点,焦点F1,F2在x轴上,离心率e=$\frac{1}{2}$,且经过点M(1,$\frac{3}{2}$).
已知椭圆C的中心在原点,焦点F1,F2在x轴上,离心率e=$\frac{1}{2}$,且经过点M(1,$\frac{3}{2}$).