题目内容
20.已知焦点在x轴的椭圆C:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{{b}^{2}}$=1的离心率为$\frac{\sqrt{3}}{2}$(I)求椭圆C的标准方程;
(II)求椭圆C被直线y=x截得的线段长.
分析 (I)求得椭圆的a=2,运用离心率公式可得c,由a,b,c的关系可得b,进而得到椭圆方程;
(II)设直线与椭圆交于A,B两点,联立直线的方程和椭圆方程,求得交点A,B的坐标,由两点的距离公式即可得到所求值.
解答 解:(I)椭圆C:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{{b}^{2}}$=1的a=2,c=$\sqrt{4-{b}^{2}}$,
由e=$\frac{c}{a}$=$\frac{c}{2}$=$\frac{\sqrt{3}}{2}$,解得c=$\sqrt{3}$,b=1,
即有椭圆的方程为$\frac{{x}^{2}}{4}$+y2=1;
(II)设直线与椭圆交于A,B两点.
由$\left\{\begin{array}{l}{y=x}\\{{x}^{2}+4{y}^{2}=4}\end{array}\right.$,可得5x2=4,解得x=±$\frac{2\sqrt{5}}{5}$,
可得A($\frac{2\sqrt{5}}{5}$,$\frac{2\sqrt{5}}{5}$),B(-$\frac{2\sqrt{5}}{5}$,-$\frac{2\sqrt{5}}{5}$),
所以|AB|=$\sqrt{(\frac{4\sqrt{5}}{5})^{2}+(\frac{4\sqrt{5}}{5})^{2}}$=$\frac{4\sqrt{10}}{5}$.
点评 本题考查椭圆的方程的求法,注意运用离心率公式和a,b,c的关系,考查弦长的求法,注意联立直线方程和椭圆方程,求得交点,运用两点的距离公式,属于基础题.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
11.已知函数f(x)=3cos($\frac{π}{4}$-ωx)(ω>0),函数f(x)相邻两个零点之间的绝对值为$\frac{π}{2}$,则下列为函数f(x)的单调递减区间的是( )
| A. | [0,$\frac{π}{2}$] | B. | [$\frac{π}{2}$,π] | C. | [$\frac{π}{8}$,$\frac{5π}{8}$] | D. | [$\frac{5π}{8}$,$\frac{9π}{8}$] |
15.在复平面内,复数$\frac{1-2i}{2+i}$对应的点的坐标为( )
| A. | ($\frac{4}{5}$,$\frac{3}{5}$) | B. | ($\frac{4}{5}$,-$\frac{3}{5}$) | C. | (0,1) | D. | (0,-1) |
5.已知全集U=R,集合A={0,1,2,3,4},B={x|0<x<3},则如图中阴影部分所表示的集合为( )
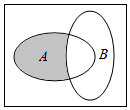

| A. | {0,1,2} | B. | {0,1,} | C. | {0,3,4} | D. | {3,4} |
12.如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则该几何体的表面积为( )
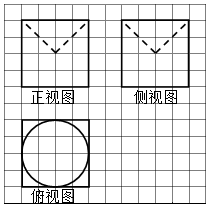

| A. | 96 | B. | $80+4\sqrt{2}π$ | C. | $96+4(\sqrt{2}-1)π$ | D. | $96+4(2\sqrt{2}-1)π$ |
9.已知某几何体的三视图如图所示,则该几何体的体积为( )


| A. | $\frac{8π}{3}$ | B. | 3π | C. | $\frac{10π}{3}$ | D. | $\frac{11π}{3}$ |