题目内容
已知函数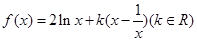 。
。
(1)当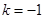 时,求函数
时,求函数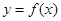 的单调区间;
的单调区间;
(2)求证:当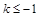 时,对所有的
时,对所有的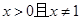 都有
都有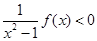 成立.
成立.
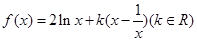 。
。(1)当
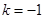 时,求函数
时,求函数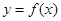 的单调区间;
的单调区间;(2)求证:当
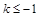 时,对所有的
时,对所有的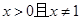 都有
都有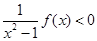 成立.
成立.(1)当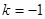 时,
时,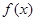 的减区间为
的减区间为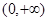 ,无增区间;
,无增区间;
(2)通过求导数,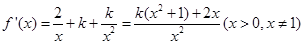 ,
,
由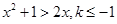 ,得到
,得到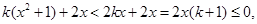
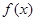 在
在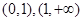 均为单调减函数.
均为单调减函数.
分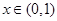 和
和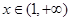 讨论得证.
讨论得证.
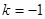 时,
时,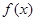 的减区间为
的减区间为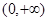 ,无增区间;
,无增区间;(2)通过求导数,
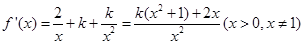 ,
,由
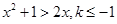 ,得到
,得到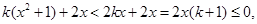
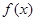 在
在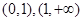 均为单调减函数.
均为单调减函数.分
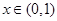 和
和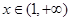 讨论得证.
讨论得证.试题分析:(1)根据
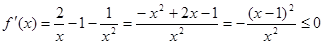
确定
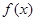 的减区间为
的减区间为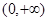 ,无增区间;
,无增区间;(2)通过求导数,
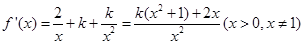 ,
,由
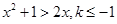 ,得到
,得到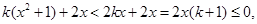
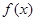 在
在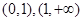 均为单调减函数.
均为单调减函数.分
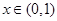 和
和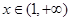 讨论得证.
讨论得证.试题解析:(1)当
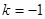 时,
时,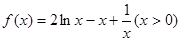
∵
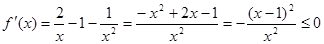
∴
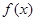 的减区间为
的减区间为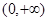 ,无增区间;
,无增区间;(2)证明:
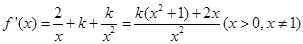 ,
,因为,
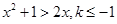 ,所以,
,所以,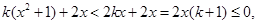
故
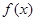 在
在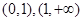 均为单调减函数.
均为单调减函数.当
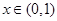 时,
时, ,而
,而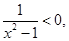 则
则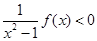 ;
;当
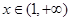 时,
时,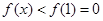 ,而
,而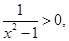 则
则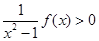 ;
;综上知,当
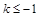 时,对所有的
时,对所有的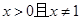 都有
都有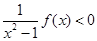 成立.
成立.
练习册系列答案
相关题目
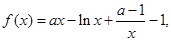 试讨论
试讨论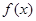 的单调性.
的单调性.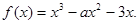
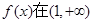 上是增函数,求实数
上是增函数,求实数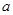 的取值范围.
的取值范围.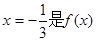 的一个极值点,求
的一个极值点,求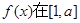 上的最大值.
上的最大值.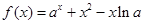 ,
,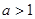
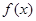 在
在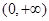 上的单调递增;
上的单调递增;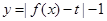 有三个零点,求
有三个零点,求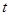 的值;
的值;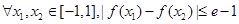 恒成立,求a的取值范围。
恒成立,求a的取值范围。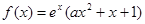 .
.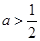 时,求
时,求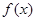 的单调区间;
的单调区间;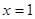 时,
时,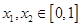 时,求
时,求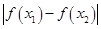 的取值范围.
的取值范围.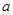 为实数,函数
为实数,函数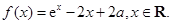
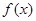 的单调区间与极值;
的单调区间与极值;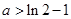 且
且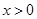 时,
时,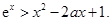
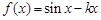 存在极值,则实数
存在极值,则实数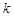 的取值范围是( )
的取值范围是( )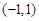
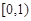
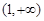
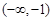
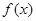 为定义在
为定义在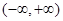 上的可导函数,
上的可导函数,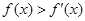 对于
对于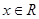 恒成立,且
恒成立,且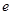 为自然对数的底数,则( )
为自然对数的底数,则( )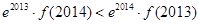
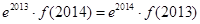
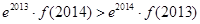
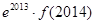 与
与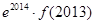 的大小不能确定
的大小不能确定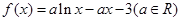 .
.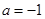 ,求函数
,求函数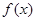 的单调区间;
的单调区间; 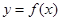 的图象在点(2,f(2))处的切线的倾斜角为
的图象在点(2,f(2))处的切线的倾斜角为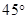 ,对于任意的
,对于任意的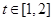 ,函数
,函数
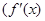 是
是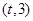 上总不是单调函数,求
上总不是单调函数,求 的取值范围;
的取值范围;  .
.