题目内容
已知函数f(x)=
cos2x+sinxcosx-
(1)求函数f(x)的单调递增区间;
(2)若x∈[0,
],求函数f(x)的取值范围;
(3)函数f(x)的图象经过怎样的平移可使其对应的函数成为奇函数?
| 3 |
| ||
| 2 |
(1)求函数f(x)的单调递增区间;
(2)若x∈[0,
| π |
| 4 |
(3)函数f(x)的图象经过怎样的平移可使其对应的函数成为奇函数?
考点:三角函数中的恒等变换应用,函数y=Asin(ωx+φ)的图象变换
专题:三角函数的求值
分析:(1)化简可得f(x)=sin(2x+
)由-
+2kπ≤2x+
≤
+2kπ解不等式可得;
(2)由x∈[0,
]可得2x+
∈[
,
],由三角函数的性质易得值域;
(3)将f(x)的图象上所有的点向右平移
个单位长度即可.
| π |
| 3 |
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
(2)由x∈[0,
| π |
| 4 |
| π |
| 3 |
| π |
| 3 |
| 5π |
| 6 |
(3)将f(x)的图象上所有的点向右平移
| π |
| 6 |
解答:
解:(1)化简可得f(x)=
cos2x+sinxcosx-
=
•
+
sin2x-
=
cos2x+
sin2x=sin(2x+
)
由-
+2kπ≤2x+
≤
+2kπ可得-
+kπ≤x≤
+kπ,
∴f(x)的单调递增区间为:[-
+kπ,
+kπ](k∈Z).
(2)∵x∈[0,
],∴2x+
∈[
,
],
∴当2x+
=
即x=
时,f(x)max=1,
当2x+
=
即x=
时,f(x)min=
,
∴
≤f(x)≤1.
(3)将f(x)的图象上所有的点向右平移
个单位长度得到y=sin2x的图象,其对应的函数即为奇函数.(答案不唯一)
| 3 |
| ||
| 2 |
=
| 3 |
| 1+cos2x |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
=
| ||
| 2 |
| 1 |
| 2 |
| π |
| 3 |
由-
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
| 5π |
| 12 |
| π |
| 12 |
∴f(x)的单调递增区间为:[-
| 5π |
| 12 |
| π |
| 12 |
(2)∵x∈[0,
| π |
| 4 |
| π |
| 3 |
| π |
| 3 |
| 5π |
| 6 |
∴当2x+
| π |
| 3 |
| π |
| 2 |
| π |
| 12 |
当2x+
| π |
| 3 |
| 5π |
| 6 |
| π |
| 4 |
| 1 |
| 2 |
∴
| 1 |
| 2 |
(3)将f(x)的图象上所有的点向右平移
| π |
| 6 |
点评:本题考查三角函数中的恒等变换,涉及三角函数的单调性和图象变换,属基础题.

练习册系列答案
相关题目
下列给出的赋值语句中正确的是( )
| A、x=3 | B、3=x |
| C、x-3=0 | D、3-x=0 |
已知集合M={-1,0,1,3},N={-2,1,2,3},则M∩N=( )
| A、{-1,1} | B、{1,2,3} |
| C、{1,3} | D、φ |
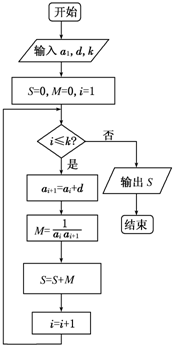 已知等差数列{an}的各项均为正数,观察如图所示的程序框图,当k=5,k=10时,分别有S=
已知等差数列{an}的各项均为正数,观察如图所示的程序框图,当k=5,k=10时,分别有S=| 5 |
| 11 |
| 10 |
| 21 |
| A、an=2n+1 |
| B、an=2n+3 |
| C、an=2n-1 |
| D、an=2n-3 |
设a>0,b>0若log2a与log2b的等差中项为2,则
+
的最小值为( )
| 1 |
| a |
| 2 |
| b |
| A、8 | ||||
B、
| ||||
C、2
| ||||
D、
|