题目内容
15．
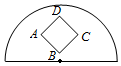如图，在半径为1的半圆内，放置一个边长为$\frac{1}{2}$的正方形ABCD，向半圆内任取一点，则该点落在正方形内的槪率为（ ）| A． | $\frac{1}{π}$ | B． | $\frac{1}{2π}$ | C． | $\frac{2}{π}$ | D． | $\frac{π}{4}$ |
分析 根据几何概型的概率公式求出对应的区域面积即可．
解答 解：半圆的面积S=$\frac{π}{2}$，正方形的面积S1=$\frac{1}{2}×\frac{1}{2}=\frac{1}{4}$，
则对应的概率P=$\frac{{S}_{1}}{S}=\frac{\frac{1}{4}}{\frac{π}{2}}$=$\frac{1}{2π}$，
故选：B
点评 本题主要考查几何概型的概率的计算，求出对应区域的面积是解决本题的关键．
练习册系列答案
相关题目
10．已知直线l：x+y-4=0，定点P（2，0），E，F分别是直线l和y轴上的动点，则△PEF的周长的最小值为（ ）
| A． | 2$\sqrt{10}$ | B． | 6 | C． | 3$\sqrt{3}$ | D． | 2$\sqrt{5}$ |
20．已知sin2θ=$\frac{3}{7}$，则cos2（θ-$\frac{π}{4}$）的值是（ ）
| A． | $\frac{2}{7}$ | B． | $\frac{3}{7}$ | C． | $\frac{4}{7}$ | D． | $\frac{5}{7}$ |