题目内容
7．已知向量$\overrightarrow{a}$=（3，4），$\overrightarrow{b}$=（2，x），若$\overrightarrow{a}$•$\overrightarrow{b}$=2|$\overrightarrow{a}$|，则实数x等于（ ）| A． | -1 | B． | 1 | C． | 2 | D． | 11 |
分析 进行数量积的坐标运算求出$\overrightarrow{a}•\overrightarrow{b}$，根据坐标求出$|\overrightarrow{a}|$，从而由$\overrightarrow{a}•\overrightarrow{b}=2|\overrightarrow{a}|$便可建立关于x的方程，解方程便得实数x的值．
解答 解：$\overrightarrow{a}•\overrightarrow{b}=6+4x，|\overrightarrow{a}|=5$；
∴由$\overrightarrow{a}•\overrightarrow{b}=2|\overrightarrow{a}|$得：
6+4x=10；
∴x=1．
故选：B．
点评 考查数量积的坐标运算，以及根据向量的坐标求向量的长度．
练习册系列答案
名校通行证有效作业系列答案
相关题目
18．投掷一枚均匀硬币和一枚均匀骰子各一次，记“硬币数字一面向上”为事件A，“骰子向上的点数是偶数”为事件B，则事件A，B中至少有一件发生的概率是（ ）
| A． | $\frac{1}{4}$ | B． | $\frac{1}{2}$ | C． | $\frac{3}{4}$ | D． | $\frac{7}{12}$ |
15．
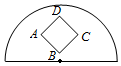如图，在半径为1的半圆内，放置一个边长为$\frac{1}{2}$的正方形ABCD，向半圆内任取一点，则该点落在正方形内的槪率为（ ）
如图，在半径为1的半圆内，放置一个边长为$\frac{1}{2}$的正方形ABCD，向半圆内任取一点，则该点落在正方形内的槪率为（ ）| A． | $\frac{1}{π}$ | B． | $\frac{1}{2π}$ | C． | $\frac{2}{π}$ | D． | $\frac{π}{4}$ |
2．已知二项式（3-x）n（n∈N*）展开式中所有项的系数之和为a，所有项的系数的绝对值之和为b，则$\frac{b}{a}$+$\frac{a}{b}$的最小值为（ ）
| A． | $\frac{9}{2}$ | B． | 2 | C． | $\frac{13}{6}$ | D． | $\frac{5}{2}$ |
19．函数f（x）=sin（ωx+φ）（其中|φ|＜$\frac{π}{2}$）的图象如图所示，则f（2016π）=（ ）
| A． | -$\frac{\sqrt{3}}{2}$ | B． | $\frac{\sqrt{3}}{2}$ | C． | -$\frac{1}{2}$ | D． | $\frac{1}{2}$ |