题目内容
6.实数x、y满足条件$\left\{\begin{array}{l}{x-y+1≥0}\\{y+1≥0}\\{x+y+1≤0}\end{array}\right.$,那么μ=22x-y+2的最大值为( )| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
分析 画出可行域$\left\{\begin{array}{l}{x-y+1≥0}\\{y+1≥0}\\{x+y+1≤0}\end{array}\right.$,可得A(0,-1).令2x-y+2=t,则y=2x+2-t,当此直线经过点A时,t取得最大值.
解答 解:画出可行域$\left\{\begin{array}{l}{x-y+1≥0}\\{y+1≥0}\\{x+y+1≤0}\end{array}\right.$, A(0,-1).
A(0,-1).
令2x-y+2=t,
则y=2x+2-t,当此直线经过点A时,t取得最大值t=0-(-1)+2=3.
那么μ=22x-y+2的最大值为:μ=23=8.
故选:D.
点评 本题考查了线性规划、直线方程、指数函数的单调性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
16.已知集合A={x∈Z|-1<x<3},B={x∈R|x2+x-6<0},则A∩B=( )
| A. | {x|-1<x<2} | B. | {x|-3<x<3} | C. | {0,1} | D. | {0,1,2} |
11.已知向量$\overrightarrow{a}$=(2,x),$\overrightarrow{b}$=(-1,2),且$\overrightarrow{a}$⊥$\overrightarrow{b}$,则x的值是( )
| A. | 1 | B. | 2 | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
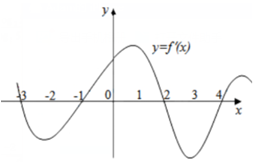 如图是y=f(x)的导函数的图象,现有四种说法:
如图是y=f(x)的导函数的图象,现有四种说法: