题目内容
5.直线kx-y+2-k=0与kx-y-4k-2=0之间的距离最大时k的值是$\frac{3}{4}$.分析 求出直线kx-y+2-k=0过定点A,直线kx-y-4k-2=0过定点B,线段AB的长就是两直线的最大距离,
由此求出直线的斜率k的值.
解答 解:直线kx-y+2-k=0可化为k(x-1)-y+2=0,
则该直线过定点A(1,2);
又直线kx-y-4k-2=0可化为k(x-4)-y-2=0,
则该直线过定点B(4,-2),如图所示: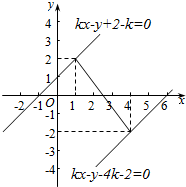
当直线kx-y+2-k=0与kx-y-4k-2=0之间的距离最大时,
两直线与直线AB垂直,
又AB的斜率为kAB=$\frac{-2-2}{4-1}$=-$\frac{4}{3}$,
∴k•(-$\frac{4}{3}$)=-1,
解得k=$\frac{3}{4}$.
故答案为:$\frac{3}{4}$.
点评 本题考查了直线方程的应用问题,也考查了数形结合与转化思想的应用问题,是基础题目.

练习册系列答案
相关题目
15.在△ABC中,若sin(B-C)=1+2sin(A+B)cos(A+C),则△ABC的形状一定是( )
| A. | 等边三角形 | B. | 直角三角形 | ||
| C. | 钝角三角形 | D. | 不含60°的等腰三角形 |
13.cos21°+cos22°+cos23°+…+cos290°的值为( )
| A. | 90 | B. | 45 | C. | 44.5 | D. | 44 |