题目内容
在△ABC中，角A，B，C的对角边分别为a，b，c，B=
，cosA=
，b=
（1）求sinC的值
（2）求△ABC的面积．
| π |
| 3 |
| 4 |
| 5 |
| 3 |
（1）求sinC的值
（2）求△ABC的面积．
考点：正弦定理,余弦定理
专题：计算题,三角函数的求值,解三角形
分析：（1）运用同角的平方关系和两角和的正弦公式计算即可得到；
（2）运用正弦定理和三角形的面积公式计算即可得到．
（2）运用正弦定理和三角形的面积公式计算即可得到．
解答：
解：（1）由cosA=
，得sinA=
=
，
即有sinC=sin（A+B）=sinAcosB+cosAsinB=
×
+
×
=
；
（2）由正弦定理可得，a=
=
=
，
则ABC的面积为S=
absinC=
×
×
×
=
．
| 4 |
| 5 |
1-
|
| 3 |
| 5 |
即有sinC=sin（A+B）=sinAcosB+cosAsinB=
| 3 |
| 5 |
| 1 |
| 2 |
| 4 |
| 5 |
| ||
| 2 |
=
3+4
| ||
| 10 |
（2）由正弦定理可得，a=
| bsinB |
| sinA |
| ||||||
|
| 5 |
| 2 |
则ABC的面积为S=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
| 3 |
3+4
| ||
| 10 |
=
3
| ||
| 8 |
点评：本题考查正弦定理和面积公式的运用，考查两角和的正弦公式和同角的平方关系的运用，属于基础题．
练习册系列答案
相关题目
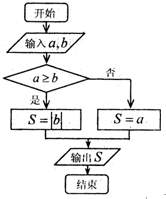定义某种运算?，a?b的运算原理如图所示：设f（x）=（0?x）x，则f（x）在区间[-2，2]上的最小值为（ ）| A、-2 | B、-4 | C、2 | D、-8 |
下列命题中是假命题的是（ ）
| A、?a，b∈R*，lg（a+b）≠lga+lgb |
| B、?φ∈R，使得函数f（x）=sin（2x+φ）是偶函数 |
| C、?α，β∈R，使得cos（α+β）=cosα+cosβ |
| D、?m∈R，使f（x）=（m-1）•x m2-2m+3是幂函数，且在（0，+∞）上递减 |