题目内容
已知F1,F2是椭圆
+
=1(a>b>0)的左,右焦点,点P是椭圆在y轴右侧上的点,且∠F1PF2=
,记线段PF1与y轴的交点为Q,O为坐标原点,若△F1OQ与四边形OF2PQ的面积之比为1:2,则该椭圆的离心率等于 .
| x2 |
| a2 |
| y2 |
| b2 |
| π |
| 2 |
考点:椭圆的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:先利用PF1与轴的交点为Q,△F1OQ与四边形OF2PQ的面积之比为1:2,点F1(-c,0),求得点P的坐标,代入椭圆标准方程即可得关于a、b、c的等式,从而求得椭圆离心率.
解答:
解: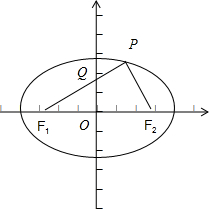 设Q(0,m),P(x,y)
设Q(0,m),P(x,y)
∵△F1OQ与四边形OF2PQ的面积之比为1:2,
∴△F1OQ与三角形PF1F2的面积之比为1:3
∴
×c×m=
×
×2c×y,∴m=
y
又∵
=
∴x=
,
∵∠F1PF2=
,
∴
×
=-1,
∴y2=
c2
将x=
和y2=
c2代入椭圆方程化简得e2+
=4,解得e=
-1
故答案为:
-1.
 设Q(0,m),P(x,y)
设Q(0,m),P(x,y)∵△F1OQ与四边形OF2PQ的面积之比为1:2,
∴△F1OQ与三角形PF1F2的面积之比为1:3
∴
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
又∵
| y |
| x+c |
| m |
| c |
∴x=
| c |
| 2 |
∵∠F1PF2=
| π |
| 2 |
∴
| y |
| x+c |
| y |
| x-c |
∴y2=
| 3 |
| 4 |
将x=
| c |
| 2 |
| 3 |
| 4 |
| 3e2 |
| 1-e2 |
| 3 |
故答案为:
| 3 |
点评:本题主要考查了椭圆的标准方程及其几何性质,特别是椭圆离心率的求法,利用已知几何条件建立关于a、b、c的等式,是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知变量x,y满足约束条件
,则目标函数z=2x+y的取值范围是( )
|
| A、[-13,5] |
| B、[-13,7] |
| C、[0,7] |
| D、[5,7] |
 如图,过点P作圆O的割线PBA与切线PE,E为切点,连接AE,BE,∠APE的平分线与AE,BE分别交于点C,D,若∠AEB=30°,则∠PCE=( )
如图,过点P作圆O的割线PBA与切线PE,E为切点,连接AE,BE,∠APE的平分线与AE,BE分别交于点C,D,若∠AEB=30°,则∠PCE=( )| A、30° | B、45° |
| C、60° | D、75° |
 将一批工件(在40mm-100mm之间)分成六段:[40,50),[50,60),…,[90,100),得到如图的频率分布直方图,则图中实数a的值为( )
将一批工件(在40mm-100mm之间)分成六段:[40,50),[50,60),…,[90,100),得到如图的频率分布直方图,则图中实数a的值为( )| A、0.4 | B、0.3 |
| C、0.04 | D、0.03 |
为了得到函数y=
sinxcosx+sin2x-
的图象,可以将函数y=sin2x的图象( )
| 3 |
| 1 |
| 2 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|