题目内容
20.给出下列结论:①平面α与平面β相交,它们只有有限个公共点;
②如果两个平面有三个不共线的公共点,那么这两个平面重合;
③四个侧面都全等的四棱柱为正四棱柱;
④底面是等边三角形,侧面都是等腰三角形的三棱锥是正三棱锥.
其中正确的是②.
分析 由公理4判断①;由公理2判断②;由正四棱柱的结构特征判断③;由正三棱锥的定义判断④.
解答 解:①、若两平面有公共点,就有无数个公共点,构成两平面的交线,①错误;
②、由公理2可知,如果两个平面有三个不共线的公共点,那么这两个平面重合,正确;
③、底面是菱形的直四棱柱的四个侧面都全等,不是正四棱柱,③错误;
④、三条侧棱中仅有一条不与底面边长相等,侧面都是等腰三角形,满足底面是等边三角形,侧面都是等腰三角形,这样的三棱锥不是正三棱锥,④错误.
∴正确的结论是②.
故答案为:②.
点评 本题考查命题的真假判断与应用,考查了空间几何体的结构特征,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.已知p:|x|>1,q:(x-2)(x-3)<0,则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
11.已知集合A={x∈R|x2+x-6>0},B={x∈R|-π<x<e},则( )
| A. | A∩B=∅ | B. | A∪B=R | C. | B⊆∁RA | D. | A⊆B |
5.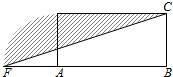 设计一个商标图案如图中阴影部分,矩形ABCD中,AB=2BC,且AB=8cm,以点A为圆心,AD为半径作圆与BA的延长线相交于点F,则商标图案的面积等于( )
设计一个商标图案如图中阴影部分,矩形ABCD中,AB=2BC,且AB=8cm,以点A为圆心,AD为半径作圆与BA的延长线相交于点F,则商标图案的面积等于( )
 设计一个商标图案如图中阴影部分,矩形ABCD中,AB=2BC,且AB=8cm,以点A为圆心,AD为半径作圆与BA的延长线相交于点F,则商标图案的面积等于( )
设计一个商标图案如图中阴影部分,矩形ABCD中,AB=2BC,且AB=8cm,以点A为圆心,AD为半径作圆与BA的延长线相交于点F,则商标图案的面积等于( )| A. | (4π+8)cm2 | B. | (4π+16)cm2 | C. | (3π+8)cm2 | D. | (3π+16)cm2 |