题目内容
14．已知f（$\frac{1}{x}$）=$\frac{x}{x+1}$，则f′（x）=（ ）| A． | $\frac{1}{1+x}$ | B． | -$\frac{1}{1+x}$ | C． | $\frac{1}{（1+x）^{2}}$ | D． | -$\frac{1}{（1+x）^{2}}$ |
分析 先利用换元法，求出f（x）的解析式，再根据导数的运算法则计算即可．
解答 解：f（$\frac{1}{x}$）=$\frac{x}{x+1}$=$\frac{1}{1+\frac{1}{x}}$，
令$\frac{1}{x}$=t，
则f（t）=$\frac{1}{1+t}$，
∴f（x）=$\frac{1}{1+x}$，
∴f′（x）=-$\frac{1}{（1+x）^{2}}$，
故选：D．
点评 本题考查了函数解析式的求法，以及导数的运算法则，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
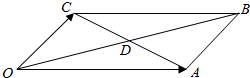在下图平行四边形?OABC中，两对角线OB与AC相交于点D，若$\overrightarrow{OA}$=（3，1），$\overrightarrow{OC}$=（1，3），则向量$\overrightarrow{OD}$的坐标是（2，2）．
5．若等比数列{an}的公比为q，n为偶数，则数列的第$\frac{n}{2}$项为（ ）
| A． | a1q${\;}^{\frac{n}{2}}$ | B． | a1q${\;}^{\frac{n-2}{2}}$ | C． | a1q${\;}^{\frac{n-1}{2}}$ | D． | a1q${\;}^{\frac{n}{2}+1}$ |