题目内容
15.已知函数f(x)=$\left\{\begin{array}{l}{2x+1(x>1)}\\{{x}^{2}(x≤1)}\end{array}\right.$,则f(2)=( )| A. | 1 | B. | 4 | C. | 5 | D. | 3 |
分析 利用分段函数的性质求解.
解答 解:∵函数f(x)=$\left\{\begin{array}{l}{2x+1(x>1)}\\{{x}^{2}(x≤1)}\end{array}\right.$,
∴f(2)=2×2+1=5.
故选:C.
点评 本题考查函数值的求法,是基础题,解题时要认真审题,注意分段函数的性质的合理运用.

练习册系列答案
相关题目
20.函数y=$\frac{2x-1}{\sqrt{3x+5}}$的定义域为( )
| A. | {x|x≥-$\frac{5}{3}$} | B. | {x|x≥-$\frac{5}{3}$且x≠$\frac{1}{2}$} | C. | {x|x>-$\frac{5}{3}$} | D. | {x|x≤-$\frac{5}{3}$} |
4.△ABC中,∠C=90°,AC=4,BC=3,D是AB的中点,E,F分别是边BC、AC上的动点,且EF=1,则$\overrightarrow{DE}$$•\overrightarrow{DF}$的最小值等于( )
| A. | $\frac{\sqrt{5}}{4}$ | B. | $\frac{15}{4}$ | C. | $\frac{17}{4}$ | D. | $\frac{\sqrt{17}}{4}$ |
5.执行如图的程序框图(n∈N*),则输出的S=( )
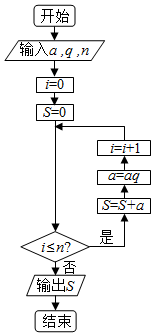

| A. | a+aq+…+aqn-1 | B. | $\frac{{a(1-{q^n})}}{1-q}$ | C. | a+aq+…+aqn | D. | $\frac{{a(1-{q^{n+1}})}}{1-q}$ |