题目内容
已知a>0,a≠1,函数f(x)=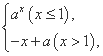 若函数f(x)在[0,2]上的最大值比最小值大
若函数f(x)在[0,2]上的最大值比最小值大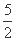 ,则a的值为 .
,则a的值为 .
 或
或
解析:若a>1,则函数f(x)在[0,1]递增,[1,2]递减,
∴f(x)max=f(1)=a,
f(x)min=f(0)=1或f(x)min=f(2)= a-2,
∴ 或
或
故a= .
.
若0<a<1,
则f(x)在[0,1]递减,(1,2]递减,
∴f(x)max=f(0)=1,f(x)min=f(2)=a-2,
∴1-(a-2)= 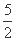 ,得a=
,得a= ,
,
综上a= 或a=
或a= .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 则f(x)的值域是( )
则f(x)的值域是( ) ∪(1,+∞) (B)[0,+∞)(C)
∪(1,+∞) (B)[0,+∞)(C) (D)
(D) ∪(2,+∞)
∪(2,+∞)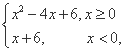 则不等式f(x)>f(1)的解集是( )
则不等式f(x)>f(1)的解集是( ) (x>0,a>0)在x=3时取得最小值,则a= .
(x>0,a>0)在x=3时取得最小值,则a= .