题目内容
f(x)=sin(
x+
),g(x)与f(x)图象关于直线x=π对称,求g(x).
| 1 |
| 2 |
| π |
| 6 |
考点:正弦函数的对称性
专题:三角函数的图像与性质
分析:在函数g(x)的图象上任意取一点A(x,y),根据点A关于直线x=π的对称点B(2π-x,y)在函数f(x)=sin(
x+
)的图象上,求得g(x)的解析式.
| 1 |
| 2 |
| π |
| 6 |
解答:
解:在函数g(x)的图象上任意取一点A(x,y),则点A关于直线x=π的对称点B(2π-x,y)在函数f(x)=sin(
x+
)的图象上,
∴y=sin[
(2π-x)+
]=sin(π-
+
)=sin(
-
),
故g(x)的解析式为 g(x)=sin(
-
).
| 1 |
| 2 |
| π |
| 6 |
∴y=sin[
| 1 |
| 2 |
| π |
| 6 |
| x |
| 2 |
| π |
| 6 |
| x |
| 2 |
| π |
| 6 |
故g(x)的解析式为 g(x)=sin(
| x |
| 2 |
| π |
| 6 |
点评:本题主要考查利用函数的图象的对称性求函数的解析式,属于基础题.

练习册系列答案
相关题目
已知m、n是两条不同的直线,α、β是两个不同的平面,则下列命题正确的是( )
| A、若α⊥β,m∥α,则m⊥β |
| B、若m∥α,n∥β,且m∥n,则α∥β |
| C、若m⊥β,α⊥β,则m∥α |
| D、若m⊥α,n⊥β,且m⊥n,则α⊥β |
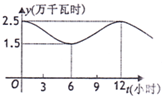 某企业一天中不同时刻用电量y(单位:万千瓦时)关于时间t(0≤t≤24,单位:小时)的函数y=f(t)近似地满足f(t)=Asin(ωt+φ)+B,(A>0,ω>0,0<φ<π),如图是该企业一天中在0点到12点时间段用电量y与时间t的大致图象.
某企业一天中不同时刻用电量y(单位:万千瓦时)关于时间t(0≤t≤24,单位:小时)的函数y=f(t)近似地满足f(t)=Asin(ωt+φ)+B,(A>0,ω>0,0<φ<π),如图是该企业一天中在0点到12点时间段用电量y与时间t的大致图象.