题目内容
19.函数$f(x)=cos(ln\frac{x-1}{x+1})$的图象大致为( )| A. | 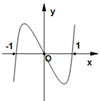 | B. | 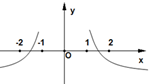 | ||
| C. | 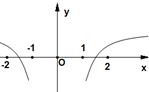 | D. | 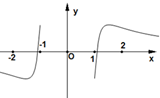 |
分析 根据函数的定义域,奇偶性,以及函数值的变化趋势,即可判断.
解答 解:∵$\frac{x-1}{x+1}$>0,
∴x>1或x<1,
∴函数f(x)的定义域为(-∞,-1)∪(1,+∞),
∵g(x)=ln$\frac{x-1}{x+1}$,
∴g(-x)=ln$\frac{-x-1}{-x+1}$=ln$\frac{x+1}{x-1}$=-ln$\frac{x-1}{x+1}$=-g(x),
∴g(x)为奇函数,
∵y=cosx为偶函数,
∴f(-x)=f(x),
∴f(x)为偶函数,
当x→+∞时,g(x)→0,
∴f(x)→1,
故选:C.
点评 本题考查了函数的图象和识别,关键是掌握函数的定义域,值域,奇偶性,单调性,以及函数值的变化趋势,属于中档题.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
11.已知定义在R上的函数f(x)满足f(x)=2f(x+2),当x∈[0,2)时,f(x)=x2-2x.若x∈[4,6)时,不等式f(x)≥$\frac{t}{4}$-$\frac{1}{2t}$恒成立,则t的取值范围为( )
| A. | [-2,0)∪[1,+∞) | B. | (-∞,2]∪(0,1] | C. | [-2,0)∪(0,1) | D. | [-2,0)∪(0,1] |