题目内容
已知点A(-2,0)和圆O:x2+y2=4,AB是圆O的直经,从左到右M、O和N依次是AB的四等分点,P(异于A、B)是圆0上的动点,PD⊥AB,交AB于D,
=λ
,直线PA与BE交于C,|CM|+|CN|为定值.
(1)求λ的值及点C的轨迹曲线E的方程.
(2)若点Q、R是曲线E上不同的点,且PQ、PR与曲线E相切,求△OQR面积的最小值.
| PE |
| ED |
(1)求λ的值及点C的轨迹曲线E的方程.
(2)若点Q、R是曲线E上不同的点,且PQ、PR与曲线E相切,求△OQR面积的最小值.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)由已知得B(2,0),M(-1,0),N(1,0),设P(x0,y0),C(x,y),则E(x0,
),由
=
,由此能求出λ的值和点C的轨迹曲线E的方程.
(2).设Q(x1,y1),R(x2,y2),设直线QR的方程为y=kx+m,直线QR的方程为
+
=1,由y=kx+m与椭圆
+
=1,x≠2联立,得(4k2+3)x2-8kmx+4m2-12=0,由此利用韦达定理、点到直线距离公式结合已知条件能求出△OQR面积的最小值.
| y0 |
| 1+λ |
| y2 |
| x2-4 |
| ||
| x02-4 |
(2).设Q(x1,y1),R(x2,y2),设直线QR的方程为y=kx+m,直线QR的方程为
| x0x |
| 4 |
| y0y |
| 3 |
| x2 |
| 4 |
| y2 |
| 3 |
解答:
解:(1)∵点A(-2,0)和圆O:x2+y2=4,AB是圆O的直经,
∴B(2,0),∵从左到右M、O和N依次是AB的四等分点,∴M(-1,0),N(1,0),
设P(x0,y0),C(x,y),则E(x0,
),
直线PA与BE交于C,
故x≠±2,
=
,①
且
=
,②…(2分)
①②相乘得
=
,
又因为点P(异于A,B)是圆O上的动点,
故
=-
,
即
+
=1,要使|CM|+|CN|为定值,
则4-
=1,解得λ=
,此时
+
=1,x≠±2,
即λ=
时,点C的轨迹曲线E的方程为
+
=1,x≠2.…(5分)
(2).设Q(x1,y1),R(x2,y2),又因为点P(异于A,B) 是圆O上的动点,
故直线QR斜率存在,设直线QR的方程为y=kx+m,
则PQ、PR的方程分别为
+
=1,
+
=1,
所以
+
=1,
+
=1,
故直线QR的方程为
+
=1,
比较系数,得k=-
,m=
,
即y0=
,x0=-
,∴4m2=16k2+9,③…(7分)
另一方面,由y=kx+m与椭圆
+
=1,x≠2联立,
得(4k2+3)x2-8kmx+4m2-12=0,
于是得x1+x2=
,④,x1x2=
,⑤…(9分)
∴|QR|=
|x1-x2|,又因为O到QR的距离为d=
,
所以△OQR的面积:
S=
|QR|•d=
|x1-x2|=
,
将③④⑤代入消去k,得S=
=
,其中|m|=|
|∈[
,+∞).…(11分)
∴f(t)=
在[
,+∞)是减函数,于是当t=|m|=
时,
Smin=[f(t)]min=f(
)=
.…(13分)
∴B(2,0),∵从左到右M、O和N依次是AB的四等分点,∴M(-1,0),N(1,0),
设P(x0,y0),C(x,y),则E(x0,
| y0 |
| 1+λ |
直线PA与BE交于C,
故x≠±2,
| y |
| x+2 |
| y0 |
| x0+2 |
且
| y |
| x-2 |
| ||
| x0-2 |
①②相乘得
| y2 |
| x2-4 |
| ||
| x02-4 |
又因为点P(异于A,B)是圆O上的动点,
故
| y2 |
| x2-4 |
| 1 |
| 1+λ |
即
| x2 |
| 4 |
| y2 | ||
|
则4-
| 4 |
| 1+λ |
| 1 |
| 3 |
| x2 |
| 4 |
| y2 |
| 3 |
即λ=
| 1 |
| 3 |
| x2 |
| 4 |
| y2 |
| 3 |
(2).设Q(x1,y1),R(x2,y2),又因为点P(异于A,B) 是圆O上的动点,
故直线QR斜率存在,设直线QR的方程为y=kx+m,
则PQ、PR的方程分别为
| xx1 |
| 4 |
| yy1 |
| 3 |
| xx2 |
| 4 |
| yy2 |
| 3 |
所以
| x0x1 |
| 4 |
| y0y1 |
| 3 |
| x0x2 |
| 4 |
| y0y2 |
| 3 |
故直线QR的方程为
| x0x |
| 4 |
| y0y |
| 3 |
比较系数,得k=-
| 3x0 |
| 4y0 |
| 3 |
| y0 |
即y0=
| 3 |
| m |
| 4k |
| m |
另一方面,由y=kx+m与椭圆
| x2 |
| 4 |
| y2 |
| 3 |
得(4k2+3)x2-8kmx+4m2-12=0,
于是得x1+x2=
| 8km |
| 4k2+3 |
| 4m2-12 |
| 4k2+3 |
∴|QR|=
| k2+1 |
| |m| | ||
|
所以△OQR的面积:
S=
| 1 |
| 2 |
| |m| |
| 2 |
| 1 |
| 2 |
| m2[(x1+x2)2-4x1x2] |
将③④⑤代入消去k,得S=
| 12|m| |
| 4m2+3 |
| 12 | ||
4|m|+
|
| 3 |
| y0 |
| 3 |
| 2 |
∴f(t)=
| 12 | ||
4|m|+
|
| 3 |
| 2 |
| 3 |
| 2 |
Smin=[f(t)]min=f(
| 3 |
| 2 |
| 3 |
| 2 |
点评:本题考查点的轨迹方程的求法,考查三角形面积的最小值的求法,解题时要认真审题,注意点到直线的距离公式的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
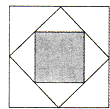 任意画一个正方形,再将这个正方形各边的中点相连得到第二个正方形,依此类推,这样一共画了3个正方形,如图所示.若向图形中随机投一点,则所投点落在第三个正方形的概率是
任意画一个正方形,再将这个正方形各边的中点相连得到第二个正方形,依此类推,这样一共画了3个正方形,如图所示.若向图形中随机投一点,则所投点落在第三个正方形的概率是