题目内容
(本小题满分12分)若数列 满足
满足 ,
, .
.
(1)设 ,问:
,问: 是否为等差数列?若是,请说明理由并求出通项
是否为等差数列?若是,请说明理由并求出通项 ;
;
(2)设 ,求
,求 的前n项和.
的前n项和.
(1)bn=3n- ;(2)Sn=
;(2)Sn= .
.
【解析】
试题分析:(1)利用 ,代入
,代入 可得bn+1-bn=
可得bn+1-bn= =3,即可得出结论;
=3,即可得出结论;
(2)确定{cn}的通项,利用裂项法,求出{cn}的前n项和.
试题解析:(1)∵bn+1-bn= =
= =3
=3
∴{bn}是公差为3的等差数列,又b1= =
= ,∴bn=3n-
,∴bn=3n- ;
;
(2)∵bn= ,∴an=
,∴an= ,由
,由 得:3an+1 an+an+1=an,
得:3an+1 an+an+1=an,
an an+1= (an-an+1),∴Cn=
(an-an+1),∴Cn= (an-an+1)
(an-an+1)
∴{Cn}的前n项和为 Sn= [(a1-a2)+(a2-a3)+…+(an-an+1)
[(a1-a2)+(a2-a3)+…+(an-an+1)
= (a1-an+1)=
(a1-an+1)= (2-
(2- ) =
) = .
.
考点:等差数列,数列求和.
考点分析: 考点1:等差数列 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目
 的夹角为
的夹角为 ,
, ( )
( ) B.
B. C.
C. D.
D.
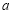 为如图所示的程序框图中输出的结果,则化简
为如图所示的程序框图中输出的结果,则化简 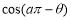 的结果是
的结果是
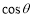 B.
B.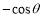 C.
C.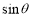 D.
D.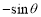
 。
。 等于( )
等于( )
 B.
B. C.
C. D.
D.
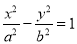 (a>0, b>0)的两条渐近线分别交于A、B两点,若P(m, 0)满足|PA|=|PB|,则该双曲线的离心率为 .
(a>0, b>0)的两条渐近线分别交于A、B两点,若P(m, 0)满足|PA|=|PB|,则该双曲线的离心率为 . 中,
中,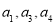 成等比数列,则公比为
成等比数列,则公比为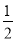 ;
;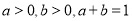 ,则
,则 的最小值为
的最小值为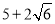 ;
; 中,已知
中,已知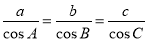 ,则
,则 .
.