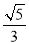题目内容
设直线x-3y+m=0(m≠0)与双曲线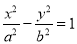 (a>0, b>0)的两条渐近线分别交于A、B两点,若P(m, 0)满足|PA|=|PB|,则该双曲线的离心率为 .
(a>0, b>0)的两条渐近线分别交于A、B两点,若P(m, 0)满足|PA|=|PB|,则该双曲线的离心率为 .
 .
.
【解析】
试题分析:双曲线 (a>0,b>0)的两条渐近线方程为
(a>0,b>0)的两条渐近线方程为 ,则
,则
与直线x-3y+m=0联立,可得A( ),B(
),B( ),
),
∴AB中点坐标为( ),
),
∵点P(m,0)满足|PA|=|PB|,
∴ ,
,
∴a=2b,
∴ ,
,
∴ .
.
故答案为: .
.
考点:直线与双曲线的位置关系,双曲线的离心率.
考点分析: 考点1:双曲线的标准方程 考点2:双曲线的几何性质 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
相关题目
 中,内角
中,内角 所对的边分别为
所对的边分别为 ,
, .
. 的大小;
的大小; 的角平分线
的角平分线 交线段
交线段 于
于 ,且
,且 ,设
,设 .
. 与
与 的关系式;
的关系式; 和
和 的面积分别为
的面积分别为 、
、 ,问当
,问当 取何值时,
取何值时, +
+ 的值最小,最小值是多少?
的值最小,最小值是多少?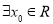 ,使得
,使得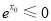
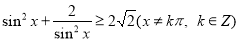

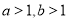 是
是 的充分不必要条件
的充分不必要条件 的部分图象如图所示,则
的部分图象如图所示,则 的解析式是( )
的解析式是( )
 B.
B.
 D.
D.
 满足
满足 ,
, .
. ,问:
,问: 是否为等差数列?若是,请说明理由并求出通项
是否为等差数列?若是,请说明理由并求出通项 ;
; ,求
,求 的前n项和.
的前n项和. =10,则
=10,则 等于( )
等于( )
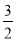 B.0 C.1 D.0或-
B.0 C.1 D.0或-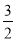
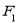 ,右焦点为
,右焦点为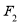 .若椭圆上存在一点
.若椭圆上存在一点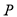 ,满足线段
,满足线段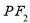 相切于以椭圆的短轴为直径的圆,切点为线段
相切于以椭圆的短轴为直径的圆,切点为线段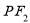 的中点,则该椭圆的离心率为 ( )
的中点,则该椭圆的离心率为 ( )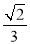 B.
B.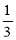 C.
C.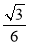 D.
D.