题目内容
已知A(-3, 0),B(0, 4),M是圆C : x2+y2-4x=0上一个动点,则△MAB的面积的最小值为( )
A.4 B.5 C.10 D.15
B.
【解析】
试题分析:由x2-4x+y2=0,得(x-2)2+y2=4,
∴圆的圆心(2,0),半径为2,
过圆心作AB所在直线的垂线,交圆于M,此时△ABM的面积最小.
直线AB的方程为4x-3y+12=0,|AB|=5,
∴圆心到直线AB的距离为 ,
,
∴△MAB的面积的最小值为 ×5×(42)=5,
×5×(42)=5,
故答案为:5.
考点:直线与圆的位置关系.
考点分析: 考点1:直线和圆的位置关系 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
(12分)在某次测验中,有6位同学的平均成绩为75分,用 表示编号为
表示编号为 的同学所得成绩,且前5位同学的成绩如下:
的同学所得成绩,且前5位同学的成绩如下:
编号 | 1 | 2 | 3 | 4 | 5 |
成绩 | 70 | 76 | 72 | 70 | 72 |
(1)求第6位同学的成绩 ,及这6位同学成绩的标准差s;
,及这6位同学成绩的标准差s;
(2)从前5位同学中,随机地选2位同学,求恰有1位同学成绩在区间(68,75)中的概率.
 满足不等式组
满足不等式组 ,那么目标函数
,那么目标函数 的最小值是_______
的最小值是_______ ,
, .
. 的值;(Ⅱ)求
的值;(Ⅱ)求 的值.
的值. 满足
满足 ,
, .
. ,问:
,问: 是否为等差数列?若是,请说明理由并求出通项
是否为等差数列?若是,请说明理由并求出通项 ;
; ,求
,求 的前n项和.
的前n项和. ,则z=2x+y的最大值为 .
,则z=2x+y的最大值为 .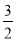 B.0 C.1 D.0或-
B.0 C.1 D.0或-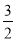


 中,
中, ,则数列
,则数列 是等比数列,命题
是等比数列,命题 “若公比
“若公比 ,则数列
,则数列 B.
B. C.
C. D.
D.