题目内容
15.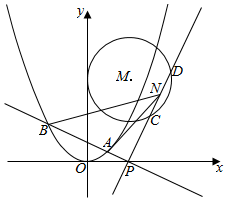 如图,抛物线E:x2=2py(p>0)的焦点为$(0,\frac{1}{4})$,圆心M在射线y=2x(x≥0)上且半径为1的圆M与y轴相切.
如图,抛物线E:x2=2py(p>0)的焦点为$(0,\frac{1}{4})$,圆心M在射线y=2x(x≥0)上且半径为1的圆M与y轴相切.(Ⅰ)求抛物线E及圆M的方程;
(Ⅱ)过P(1,0)作两条相互垂直的直线,与抛物线E相交于A,B两点,与圆M相交于C,D两点,N为线段CD的中点,当${S_{△NAB}}=\frac{3}{2}$,求AB所在的直线方程.
分析 (Ⅰ)利用抛物线E:x2=2py(p>0)的焦点为$(0,\frac{1}{4})$,圆心M在射线y=2x(x≥0)上且半径为1的圆M与y轴相切,即可求抛物线E及圆M的方程;
(Ⅱ)联立$\left\{\begin{array}{l}y={x^2}\\ y=k(x-1)\end{array}\right.$⇒x2-kx+k=0$⇒\left\{\begin{array}{l}△={k^2}-4k>0\\{x_A}+{x_B}=k\\{x_A}•{x_B}=k\end{array}\right.$,又与直线AB垂直的直线CD与圆M相交,可得k的范围,利用${S_{△NAB}}=\frac{3}{2}$,求出k,即可求AB所在的直线方程.
解答 解:(Ⅰ)抛物线E:x2=2py(p>0)的焦点为$(0,\frac{1}{4})$,∴p=$\frac{1}{2}$,∴抛物线E:y=x2,…(3分)
∵圆心M在射线y=2x(x≥0)上且半径为1的圆M与y轴相切,
∴圆M的方程:(x-1)2+(y-2)2=1; …(6分)
(Ⅱ)设直线AB的斜率为k(k显然存在且不为零)
联立$\left\{\begin{array}{l}y={x^2}\\ y=k(x-1)\end{array}\right.$⇒x2-kx+k=0$⇒\left\{\begin{array}{l}△={k^2}-4k>0\\{x_A}+{x_B}=k\\{x_A}•{x_B}=k\end{array}\right.$…(8分)
又与直线AB垂直的直线CD与圆M相交,
则$-\frac{1}{k}∈(-∞,-\sqrt{3})∪(\sqrt{3},+∞)$即$-\frac{{\sqrt{3}}}{3}<k<\frac{{\sqrt{3}}}{3}$,而k2-4k>0,故$-\frac{{\sqrt{3}}}{3}<k<0$.${S_{△NAB}}=\frac{1}{2}|AB|•|NP|=\frac{1}{2}|AB|•d$(其中d表示圆心M到直线AB的距离)
=$\frac{1}{2}\sqrt{1+{k^2}}•\sqrt{{k^2}-4k}•\frac{2}{{\sqrt{1+{k^2}}}}=\sqrt{{k^2}-4k}$…(12分)
又${S_{△NAB}}=\frac{3}{2}$,所以${k^2}-4k=\frac{9}{4}$,解得$k=-\frac{1}{2}$或$k=\frac{9}{2}$(舍)
所以AB所在的直线方程为:$y=-\frac{1}{2}(x-1)$即$y=-\frac{1}{2}x+\frac{1}{2}$.…(15分)
点评 本题考查抛物线E及圆M的方程,考查直线与抛物线的位置关系,考查三角形面积的计算,属于中档题.

 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案 名题金卷系列答案
名题金卷系列答案| A. | 相交 | B. | 相切 | C. | 相离 | D. | 以上都有可能 |
