题目内容
5．设p：函数f（x）=lg（x2-4x+a2）的定义域为R；q：a2-5a-6≥0．如果“p∨q”为真，且“p∧q”为假，求实数a的取值范围．分析 分别判断出p，q为真时的a的范围，由“p∨q”为真，“p∧q”为假，可知p，q一真一假，通过讨论求出a的范围即可．
解答 解：若p为真，则x2-4x+a2＞0恒成立，∴△=16-4a2＜0，解得 a＞2或a＜-2；…（2分）
若q为真，则a2-5a-6≥0，解得a≤-1，或a≥6． …（4分）
由“p∨q”为真，“p∧q”为假，可知p，q一真一假．…（5分）
①p真q假时，a＞2或a＜-2，且-1＜a＜6，∴2＜a＜6，…（7分）
②p假q真时，-2≤a≤2，a≤-1，或a≥6∴-2≤a≤-1…（9分）
综上，2＜a＜6，或-2≤a≤-1．∴a∈（2，6）∪[-2，-1]…（10分）
点评 本题考查了复合命题的判断，考查对数函数的性质，是一道基础题．
练习册系列答案
相关题目
13．直线x+y-3=0的倾斜角是（ ）
| A． | $\frac{π}{4}$ | B． | $\frac{π}{3}$ | C． | $\frac{3π}{4}$ | D． | $\frac{5π}{4}$ |
14．已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）与双曲线$\frac{{x}^{2}}{{m}^{2}}$-$\frac{{y}^{2}}{{n}^{2}}$=1（m＞0，n＞0）有相同的焦点（-c，0）和（c，0），若c是a，m的等比中项，n2是2m2与c2的等差中项，则椭圆的离心率是（ ）
| A． | $\frac{1}{4}$ | B． | $\frac{1}{2}$ | C． | $\frac{\sqrt{3}}{2}$ | D． | $\frac{\sqrt{2}}{2}$ |
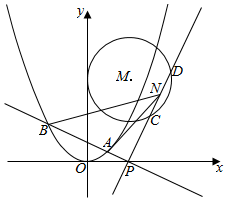如图，抛物线E：x2=2py（p＞0）的焦点为$（0，\frac{1}{4}）$，圆心M在射线y=2x（x≥0）上且半径为1的圆M与y轴相切．