题目内容
7.直线l1:(m-1)x-y+2m+1=0与圆C:(x+2)2+(y-3)2=$\sqrt{2}$的位置关系是( )| A. | 相交 | B. | 相切 | C. | 相离 | D. | 以上都有可能 |
分析 可将l1的方程整理为(x+2)m+(-x-y+1)=0,利用$\left\{\begin{array}{l}{x+2=0}\\{-x-y+1=0}\end{array}\right.$,可确定直线l过定点为圆心,即可得出结论.
解答 解:将l1的方程整理为(x+2)m+(-x-y+1)=0,
由$\left\{\begin{array}{l}{x+2=0}\\{-x-y+1=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=-2}\\{y=3}\end{array}\right.$,
∴直线l过定点(-2,3)即圆心,
∴直线l1恒与圆有两个交点,
故选:A.
点评 本题考查直线系方程的应用,考查直线与圆的位置关系,考查转化思想,确定直线l过定点.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.若集合A={1,9},B={-1,x2},则“x=3”是“A∩B={9}”的( )
| A. | 必要不充分条件 | B. | 充分不必要条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
 如图所示:四棱锥S-ABCD的底面为正方形,SD⊥底面ABCD,给出下列结论:
如图所示:四棱锥S-ABCD的底面为正方形,SD⊥底面ABCD,给出下列结论: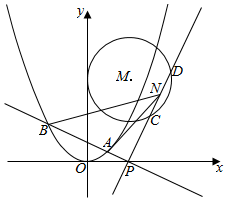 如图,抛物线E:x2=2py(p>0)的焦点为$(0,\frac{1}{4})$,圆心M在射线y=2x(x≥0)上且半径为1的圆M与y轴相切.
如图,抛物线E:x2=2py(p>0)的焦点为$(0,\frac{1}{4})$,圆心M在射线y=2x(x≥0)上且半径为1的圆M与y轴相切.