题目内容
若f(x)=x+2
f(x)dx,则
f(x)dx= .
| ∫ | 1 0 |
| ∫ | 1 0 |
考点:定积分
专题:导数的综合应用
分析:利用待定系数法结合积分的基本性质和运算即可得到结论.
解答:
解:因为
f(x)dx是个常数,设为m,
所以f(x)=x+2m,
其原函数F(x)=
x2+2mx+C(C为常数),
所以可得方程m=
+2m,解得m=-
.
故答案为:-
| ∫ | 1 0 |
所以f(x)=x+2m,
其原函数F(x)=
| 1 |
| 2 |
所以可得方程m=
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:-
| 1 |
| 2 |
点评:本题主要考查函数解析式的求解,明确
f(x)dx是个常数以及利用待定系数法是解决本题的关键.
| ∫ | 1 0 |

练习册系列答案
相关题目
已知sinα-cosα=
,则tanα+
=( )
| 1 |
| 3 |
| 1 |
| tanα |
A、
| ||
B、
| ||
C、
| ||
D、
|
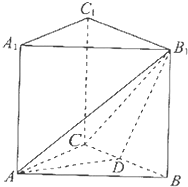 如图,在棱长均相等的正三棱柱ABC-A1B1C1中,D为BC的中点.
如图,在棱长均相等的正三棱柱ABC-A1B1C1中,D为BC的中点.