题目内容
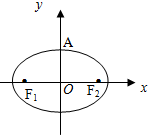 已知椭圆
已知椭圆| x2 |
| a2 |
| y2 |
| b2 |
(1)若AF1⊥AF2,求椭圆的离心率;
(2)若P(-4,3)且
| PF1 |
| PF2 |
(3)若存在一点P使∠F1PF2为钝角,求椭圆离心率的取值范围.
考点:直线与圆锥曲线的综合问题
专题:向量与圆锥曲线
分析:(1)由AF1⊥AF2,据对称性,△F1AF2为等腰直角三角形,即AO=OF2,从而得到b=c,结合a2=b2+c2
可求椭圆的离心率;
(2)由点的坐标求得
,
的坐标,代入
•
=0求得c的值,再由P(-4,3)在椭圆上联立方程组求得a2,b2的值,则椭圆方程可求;
(3)由∠F1PF2为钝角,得到
•
<0有解,转化为c2>x02+y02有解,求出x02+y02的最小值后求得椭圆离心率的取值范围.
可求椭圆的离心率;
(2)由点的坐标求得
| PF1 |
| PF2 |
| PF1 |
| PF2 |
(3)由∠F1PF2为钝角,得到
| PF1 |
| PF2 |
解答:
解:(1)如图,若AF1⊥AF2,据对称性,△F1AF2为等腰直角三角形,即AO=OF2,即b=c,
故e=
=
=
;
(2)设F1(-c,0),F2(c,0),
则有
=(-c+4,-3),
=(c+4,-3),
∵
•
=0,
∴(4-c)(4+c)+9=0,即c2=25,
又
,解得
,
即椭圆方程为
+
=1;
(3)设P(x0,y0),则|x0|<a,即0≤x02<a2,
又∠F1PF2∈(0,π).
若∠F1PF2为钝角,当且仅当
•
<0有解,
即c2>x02+y02有解,即c2>(x02+y02)min.
又
+
=1,
∴y02=b2-
x02,
∴x02+y02=b2+
x02∈[b2,a2),
即(x02+y02)min=b2.
故c2>b2,c2>a2-c2,
∴
>
,即e>
,
又0<e<1,
∴
e<1.
故e=
| c |
| a |
| c | ||
|
| ||
| 2 |
(2)设F1(-c,0),F2(c,0),
则有
| PF1 |
| PF2 |
∵
| PF1 |
| PF2 |
∴(4-c)(4+c)+9=0,即c2=25,
又
|
|
即椭圆方程为
| x2 |
| 40 |
| y2 |
| 15 |
(3)设P(x0,y0),则|x0|<a,即0≤x02<a2,
又∠F1PF2∈(0,π).
若∠F1PF2为钝角,当且仅当
| PF1 |
| PF2 |
即c2>x02+y02有解,即c2>(x02+y02)min.
又
| x02 |
| a2 |
| y02 |
| b2 |
∴y02=b2-
| b2 |
| a2 |
∴x02+y02=b2+
| c2 |
| a2 |
即(x02+y02)min=b2.
故c2>b2,c2>a2-c2,
∴
| c2 |
| a2 |
| 1 |
| 2 |
| ||
| 2 |
又0<e<1,
∴
| ||
| 2 |
点评:本题考查了直线与圆锥曲线的关系,考查了平面向量数量积在解题中的应用,体现了数学转化思想方法,解答此题的关键在于把存在一点P使∠F1PF2为钝角转化为
•
<0有解,是压轴题.
| PF1 |
| PF2 |

练习册系列答案
相关题目
类比边长为2a的正三角形内的一点到三边的距离之和为
a,对于棱长为6a的正四面体,正确的结论是( )
| 3 |
A、正四面体内部的一点到六条棱的距离的和为2
| ||
B、正四面体内部的一点到四面的距离的和为2
| ||
C、正四面体的中心到四面的距离的和为2
| ||
D、正四面体的中心到六条棱的距离的和为9
|
方程x2-2x+5=0的一个根是1-2i,则另一个根为( )
| A、1+2i | B、-1+2i |
| C、2+i | D、2-i |
下列说法中正确的有( )
①若任取x1,x2∈I,当x1<x2时,f (x1)<f (x2),则y=f (x)在I上是增函数;
②函数y=x2在R上是增函数;
③函数y=-
在定义域上是增函数;
④y=
的单调递减区间是(-∞,0)∪(0,+∞).
①若任取x1,x2∈I,当x1<x2时,f (x1)<f (x2),则y=f (x)在I上是增函数;
②函数y=x2在R上是增函数;
③函数y=-
| 1 |
| x |
④y=
| 1 |
| x |
| A、0个 | B、1个 | C、2个 | D、3个 |
如图是正方体的表面展开图,则下列描述正确的是( )


| A、BM与ED平行 |
| B、CN与BM相交 |
| C、CN与BE异面 |
| D、DM与AF平行 |
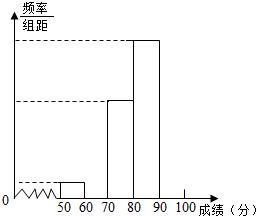 中日“钓鱼岛争端”问题越来越引起社会关注,我校对高一600名学生进行了一次“钓鱼岛”知识测试,并从中抽取了部分学生的成绩(满分100分)作为样本,绘制了下面尚未完成的频率分布表和频率分布直方图.
中日“钓鱼岛争端”问题越来越引起社会关注,我校对高一600名学生进行了一次“钓鱼岛”知识测试,并从中抽取了部分学生的成绩(满分100分)作为样本,绘制了下面尚未完成的频率分布表和频率分布直方图.