题目内容
11.若关于x的方程25-|x+1|-4•5-|x+1|-m=0有实根,求m的取值范围.变题1:设有两个命题:①关于x的方程9x+(4+a)•3x+4=0有解;②函数$f(x)={log_{2{a^2}-a}}x$是减函数.当①与②至少有一个真命题时,实数a的取值范围是$({-∞,-8}]∪({-\frac{1}{2},0})∪({\frac{1}{2},1})$
变题2:方程x2-2ax+4=0的两根均大于1,则实数a的取值范围是$[{2,\frac{5}{2}})$.
分析 令t=5-|x+1|,则t∈(0,1],方程25-|x+1|-4•5-|x+1|-m=0可化为:m=t2-4t,此时函数为减函数,进而可得m的取值范围.
变题1:令t=3x,则t∈(0,+∞),方程9x+(4+a)•3x+4=0可化为:a=-(t+$\frac{4}{t}$)-4,结合基本不等式可得:①为真时实数a的取值范围;
若函数$f(x)={log_{2{a^2}-a}}x$是减函数,则$\left\{\begin{array}{l}2{a}^{2}-a>0\\ 2{a}^{2}-a≠1\end{array}\right.$,解得:②为真时实数a的取值范围;综合可得答案;
变题2:方程x2-2ax+4=0的两根均大于1,则$\left\{\begin{array}{l}△=4{a}^{2}-16≥0\\ a>1\\ 1-2a+4>0\end{array}\right.$,解得实数a的取值范围.
解答 解:令t=5-|x+1|,则t∈(0,1],方程25-|x+1|-4•5-|x+1|-m=0可化为:m=t2-4t,
此时函数为减函数,
当t=0时,m=0,当t=1时,m=-3,
∴m∈[-3,0);
变题1:令t=3x,则t∈(0,+∞),方程9x+(4+a)•3x+4=0可化为:a=-(t+$\frac{4}{t}$)-4≤-2$\sqrt{t•\frac{4}{t}}$-4=-8,
即①为真时,a≤-8,
若函数$f(x)={log_{2{a^2}-a}}x$是减函数,则$\left\{\begin{array}{l}2{a}^{2}-a>0\\ 2{a}^{2}-a≠1\end{array}\right.$,
解得:a∈$(-\frac{1}{2},0)∪(\frac{1}{2},1)$,
若①与②至少有一个真命题,
则实数a的取值范围是:$({-∞,-8}]∪({-\frac{1}{2},0})∪({\frac{1}{2},1})$,
变题2:方程x2-2ax+4=0的两根均大于1,
则$\left\{\begin{array}{l}△=4{a}^{2}-16≥0\\ a>1\\ 1-2a+4>0\end{array}\right.$,
解得:a∈$[{2,\frac{5}{2}})$
故答案为:$({-∞,-8}]∪({-\frac{1}{2},0})∪({\frac{1}{2},1})$;$[{2,\frac{5}{2}})$
点评 本题以命题的真假判断与应用为载体,考查了方程根与函数零点的关系,指数函数与对数函数的图象和性质等知识点,难度中档.

 教学练新同步练习系列答案
教学练新同步练习系列答案| A. | 2016 | B. | 2015 | C. | 2014 | D. | 2013 |
| A. | $\sqrt{2+\sqrt{2}}$ | B. | $\sqrt{2+2\sqrt{2}}$ | C. | $\sqrt{1+\sqrt{2}}$ | D. | $\sqrt{1+2\sqrt{2}}$ |
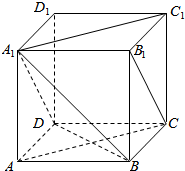 如图在正方体ABCD-A1B1C1D1中,
如图在正方体ABCD-A1B1C1D1中,