题目内容
9.一次测试中,每位考生要在8道测试题中随机抽出3道题问答,答对其中两道题即为合格.甲、乙、丙三人分别参加测试,每个人参加测试都是相互独立的,且三人都恰好会答8道题中的3道题.(1)求甲考生在一次测试中合格的概率;
(2)求三个人中恰有一人合格的概率;
(3)记X表示三个人参加测试获得合格的冉姝,写出X的分布列并求数学期望.
分析 (1)根据题意,计算甲考生在一次测试中合格的概率值;
(2)计算每个人参加测试合格的概率值,由独立重复实验的概率计算公式求出三个人中恰有一人合格的概率;
(3)由X~B(3,$\frac{2}{7}$)求出X的分布列与数学期望值.
解答 解:(1)设事件A:“甲考生在一次测试中合格”,
则P(A)=$\frac{{C}_{3}^{2}{•C}_{5}^{1}{+C}_{3}^{3}}{{C}_{8}^{3}}$=$\frac{2}{7}$,
即甲考生在一次测试中合格的概率为$\frac{2}{7}$;
(2)设事件B:“三个人中恰有一人合格”,
每个人参加测试合格的概率为$\frac{2}{7}$,
且都是相互独立的;
所以P(B)=${C}_{3}^{1}$•$\frac{2}{7}$•${(\frac{5}{7})}^{2}$=$\frac{150}{343}$;
即三个人中恰有一人合格的概率为$\frac{150}{343}$;
(3)根据题意,X的可能取值为0,1,2,3;
且X~B(3,$\frac{2}{7}$);
所以P(X=0)=${C}_{3}^{0}$•${(1-\frac{2}{7})}^{3}$=$\frac{125}{343}$,
P(X=1)=${C}_{3}^{1}$•$\frac{2}{7}$×${(1-\frac{2}{7})}^{2}$=$\frac{150}{343}$,
P(X=2)=${C}_{3}^{2}$•${(\frac{2}{7})}^{2}$×(1-$\frac{2}{7}$)=$\frac{60}{343}$,
P(X=3)=${C}_{3}^{3}$•${(\frac{2}{7})}^{3}$=$\frac{8}{343}$;
写出X的分布列为:
| X | 0 | 1 | 2 | 3 |
| P | $\frac{125}{343}$ | $\frac{150}{343}$ | $\frac{60}{343}$ | $\frac{8}{343}$ |
点评 本题考查了离散型随机变量的分布列与期望的计算问题,是基础题目.

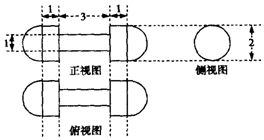 某几何体由三个圆柱和大小相同的两个半球组成,它的三视图如图所示(单位:dm),则该几何体的表面积是( )(侧视图中间有小圆)
某几何体由三个圆柱和大小相同的两个半球组成,它的三视图如图所示(单位:dm),则该几何体的表面积是( )(侧视图中间有小圆)| A. | $\frac{25π}{2}$dm2 | B. | 11πdm2 | C. | $\frac{19π}{2}$dm2 | D. | 9πdm2 |
| A. | {x|$\frac{1}{3}$≤x≤2} | B. | {x|x>2或x≤$\frac{1}{3}$} | C. | {x|$\frac{1}{3}$≤x<2} | D. | {x|x<2} |
| A. | 8个 | B. | 9个 | C. | 10个 | D. | 11个 |