题目内容
17.过抛物线y2=2px(p>0)的焦点F作倾斜角为60°的直线与抛物线交于P,Q两点,设点P关于x轴的对称点为点M,直线MQ与x轴交于点N,若△PQN的面积4$\sqrt{3}$,则实数p=$\sqrt{6}$.分析 先确定N的坐标,再根据△PQN的面积4$\sqrt{3}$,即可得出实数p的值.
解答 解:设P($\frac{{{y}_{1}}^{2}}{2p}$,y1),Q($\frac{{{y}_{2}}^{2}}{2p}$,y2),M($\frac{{{y}_{1}}^{2}}{2p}$,-y1),
设直线PQ的方程为y=$\sqrt{3}$(x-$\frac{p}{2}$),即x=$\frac{\sqrt{3}}{3}$y+$\frac{p}{2}$,
代入y2=2px可得y2-$\frac{2\sqrt{3}}{3}$py-p2=0,∴y1y2=-p2,y1+y2=$\frac{2\sqrt{3}}{3}$p.
kMQ=$\frac{2p}{{y}_{2}-{y}_{1}}$,∴直线MQ的方程为y+y1=$\frac{2p}{{y}_{2}-{y}_{1}}$(x-$\frac{{{y}_{1}}^{2}}{2p}$)
令y=0可得x=-$\frac{p}{2}$.
∴△PQN的面积S=$\frac{1}{2}$×p×|y1-y2|=$\frac{1}{2}$×p×$\sqrt{\frac{4}{3}{p}^{2}+4{p}^{2}}$=4$\sqrt{3}$,
∴p=$\sqrt{6}$.
故答案为:$\sqrt{6}$.
点评 本题考查了抛物线的定义及其性质、过焦点的弦的性质、直线与抛物线相交转化为方程联立可得根与系数的关系、斜率计算公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
7.一个三棱锥的三视图如图所示,则该三棱锥的表面积为( )
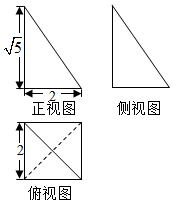

| A. | 8+$\sqrt{14}$ | B. | 8+2$\sqrt{14}$ | C. | 2+2$\sqrt{5}$+$\sqrt{14}$ | D. | 16+2$\sqrt{14}$ |
5.等差数列{an}满足a1=1,公差d=3,若an=298,则n=( )
| A. | 99 | B. | 100 | C. | 101 | D. | 102 |