题目内容
设关于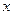 的二次函数
的二次函数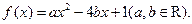
(I)设集合P={1,2, 4}和Q={-1,1,2},分别从集合P和Q中随机取一个数作为函数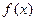 中
中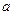 和
和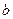 的值,求函数
的值,求函数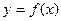 有且只有一个零点的概率;
有且只有一个零点的概率;
(II)设点(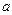 ,
,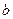 )是随机取自平面区域
)是随机取自平面区域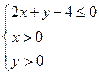 内的点,求函数
内的点,求函数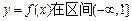 上是减函数的概率.
上是减函数的概率.
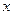 的二次函数
的二次函数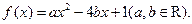
(I)设集合P={1,2, 4}和Q={-1,1,2},分别从集合P和Q中随机取一个数作为函数
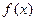 中
中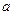 和
和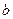 的值,求函数
的值,求函数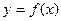 有且只有一个零点的概率;
有且只有一个零点的概率;(II)设点(
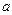 ,
,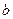 )是随机取自平面区域
)是随机取自平面区域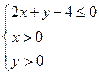 内的点,求函数
内的点,求函数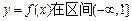 上是减函数的概率.
上是减函数的概率.(I)

(II)
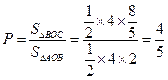
解:(I)要使函数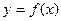 有且只有一个零点,当且仅当
有且只有一个零点,当且仅当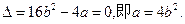 ……………………………2分
……………………………2分
分别从集合P和Q中随机取一个数作为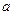 和
和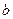 ,可以是
,可以是 共9个基本事件,其中满足
共9个基本事件,其中满足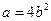 的事件有
的事件有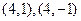 共2个,
共2个,
∴所求事件的概率为 . ……………………………6分
. ……………………………6分
(II)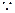 函数
函数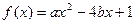 的图象的对称轴为
的图象的对称轴为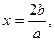
由函数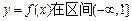 上是减函数,得
上是减函数,得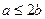 且
且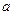 >0,....8分
>0,....8分
依条件可知试验的全部结果所构成的区域为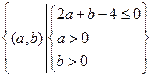 ,即三角形区域
,即三角形区域 .且
.且 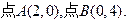 .......................................10分
.......................................10分
构成所求事件的区域为三角形区域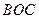 (如图).
(如图).
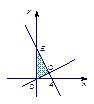
由 ……………………………12分
……………………………12分
∴所求事件的概率为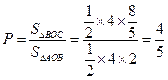 ………………… 13分
………………… 13分
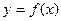 有且只有一个零点,当且仅当
有且只有一个零点,当且仅当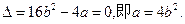 ……………………………2分
……………………………2分分别从集合P和Q中随机取一个数作为
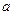 和
和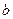 ,可以是
,可以是 共9个基本事件,其中满足
共9个基本事件,其中满足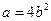 的事件有
的事件有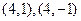 共2个,
共2个,∴所求事件的概率为
 . ……………………………6分
. ……………………………6分(II)
 函数
函数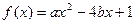 的图象的对称轴为
的图象的对称轴为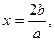
由函数
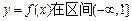 上是减函数,得
上是减函数,得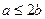 且
且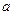 >0,....8分
>0,....8分依条件可知试验的全部结果所构成的区域为
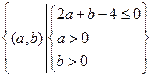 ,即三角形区域
,即三角形区域 .且
.且 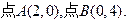 .......................................10分
.......................................10分构成所求事件的区域为三角形区域
 (如图).
(如图). 
由
 ……………………………12分
……………………………12分∴所求事件的概率为
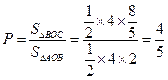 ………………… 13分
………………… 13分
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,若函数
,若函数 的极值点小于零,则( )
的极值点小于零,则( )



 的图像都过点P(2,0),且在点P处有相同的切线。
的图像都过点P(2,0),且在点P处有相同的切线。 的最小值。
的最小值。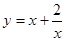 在(0,+∞)上( )
在(0,+∞)上( )
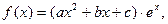 其中e为自然对数的底数,a,b,c为常数,若函数
其中e为自然对数的底数,a,b,c为常数,若函数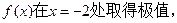 且
且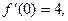
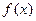 在区间[1,2]上是增函数,求实数a的取值范围。
在区间[1,2]上是增函数,求实数a的取值范围。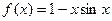 在
在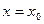 处取得极值,则
处取得极值,则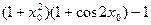 的值为( )
的值为( )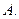 1
1 

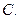 0
0 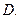 2
2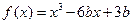 在
在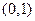 内有极小值,则实数b的取值范围是( )
内有极小值,则实数b的取值范围是( )



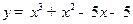 的单调增区间是___________________________。
的单调增区间是___________________________。