题目内容
6.若函数f(x)=$\frac{1}{3}$(a-1)x3+$\frac{1}{2}$ax2-$\frac{1}{4}$+$\frac{1}{5}$在其定义域内有极值点,则a的值为(-∞,$\frac{-1-\sqrt{5}}{2}$)∪($\frac{-1+\sqrt{5}}{2}$,+∞).分析 函数f(x)=$\frac{1}{3}$(a-1)x3+$\frac{1}{2}$ax2-$\frac{1}{4}$x+$\frac{1}{5}$有极值,等价于f′(x)=0有两个不相等的实数根,由此能求出a的取值范围.
解答 解:∵函数f(x)=$\frac{1}{3}$(a-1)x3+$\frac{1}{2}$ax2-$\frac{1}{4}$x+$\frac{1}{5}$,
∴f′(x)=(a-1)x2+ax-$\frac{1}{4}$,
∵函数f(x)=$\frac{1}{3}$(a-1)x3+$\frac{1}{2}$ax2-$\frac{1}{4}$x+$\frac{1}{5}$在其定义域内有极值点,
当a≠1时,f′(x)=(a-1)x2+ax-$\frac{1}{4}$=0有两个不相等的实数根,
∴△=a2-4×(a-1)×(-$\frac{1}{4}$)>0并且a-1≠0,
解得a>1或1>a>$\frac{-1+\sqrt{5}}{2}$或a<$\frac{-1-\sqrt{5}}{2}$,
当a=1时,函数f(x)=$\frac{1}{2}$x2-$\frac{1}{4}$x+$\frac{1}{5}$是二次函数,满足题意.
∴a的取值范围为(-∞,$\frac{-1-\sqrt{5}}{2}$)∪($\frac{-1+\sqrt{5}}{2}$,+∞).
故答案为:(-∞,$\frac{-1-\sqrt{5}}{2}$)∪($\frac{-1+\sqrt{5}}{2}$,+∞).
点评 本题考查函数的极大值和极小值的求法,考查实数的取值范围的求法,是中档题,解题时要认真审题,注意导数性质的合理运用.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目
17.执行如图所示的程序框图,若输出的值为-5,则判断框中可以填入的条件为( )

| A. | z>10? | B. | z≤10? | C. | z>20? | D. | z≤20? |
11.如图程序运行后,得到的a,b,c分别为( )


| A. | 2,3,2 | B. | 2,3,1 | C. | 3,2,1 | D. | 3,2,3 |
15. 阅读如图所示的程序框图,运行相应的程序.若输入的n=3,则输出的结果为( )
阅读如图所示的程序框图,运行相应的程序.若输入的n=3,则输出的结果为( )
 阅读如图所示的程序框图,运行相应的程序.若输入的n=3,则输出的结果为( )
阅读如图所示的程序框图,运行相应的程序.若输入的n=3,则输出的结果为( )| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
16.已知函数y=Asin(ωx+φ)(ω>0,-π≤φ<π)的图象如图所示,则φ的值为(
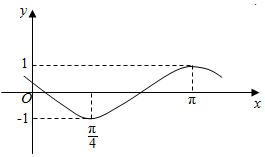

| A. | 0 | B. | -$\frac{5π}{6}$ | C. | $\frac{5π}{6}$ | D. | -$\frac{π}{6}$ |
