题目内容

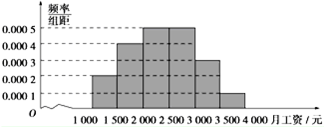
14．在正方体中ABCD-A′B′C′D′中，点E为底面ABCD上的动点，若三棱锥B-D′EC的体积最大，则点E（　　）
A．位于线段AB上B．位于线段AD上C．只能在A点D．只能在AB的中点

分析 连接BE，CE，D′E，对三棱锥B-D′EC，无论E在底面ABCD上的何位置，面BCD′的面积为定值，要使三棱锥B-D′EC的表面积最大，则侧面BCE、CAD′、BAD′的面积和最大，由此能求出结果．

解答 解：E为底面ABCD上的动点，连接BE，CE，D′E，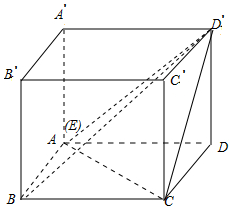
对三棱锥B-D′EC，无论E在底面ABCD上的何位置，
面BCD'的面积为定值，
要使三棱锥B-D′EC的表面积最大，
则侧面BCE、CAD′、BAD′的面积和最大，
而当E与A重合时，三侧面的面积均最大，
∴E点位于点A处时，三棱锥B-D′EC的表面积最大．
故选：C．

点评 本题考查使三棱锥的体积最大时点的位置的判断，是中档题，解题时要认真审题，注意空间思维能力的培养．

练习册系列答案
相关题目
4．一个几何体的正视图，侧视图为边长为2的正方形，其全面积为（　　）
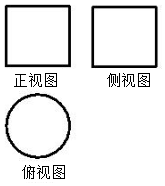
A．6πB．$8\sqrt{2}$πC．$4+4\sqrt{2}$πD．$8+4\sqrt{2}$π
5．$\frac{{cos10°（\sqrt{3}tan20°-1）}}{tan20°}$=-1．
2．某中学为了了解全校学生的上网情况，在全校采用随机抽样的方法抽取了40名学生（其中男女生人数恰好各占一半）进行问卷调查，并进行了统计，按男女分为两组，再将每组学生的月上网次数分为5组：[0，5），[5，10），[10，15），[15，20），[20，25]，得到如图所示的频率分布直方图：
（Ⅰ）写出a的值；
（Ⅱ）求在抽取的40名学生中月上网次数不少于15次的学生人数；
（Ⅲ）在抽取的40名学生中，从月上网次数不少于20次的学生中随机抽取2人，求至少抽到1名女生的概率．
9．某市统计局就某地居民的月收入调查了10000人，并根据所得数据画出样本的频率分布直方图如图所示．（每个分组包括左端点，不包括右端点，如第一组表示[1 000，1 500））

（1）求居民收入在[3 000，3 500）的频率；
（2）根据频率分布直方图估算出样本数据的平均数，众数，中位数．
19．设锐角△ABC的三个内角A，B，C的对边分别为a，b，c成等比数列，且sinAsinC=$\frac{3}{4}$，则角B=（　　）
A．$\frac{π}{6}$B．$\frac{π}{3}$C．$\frac{π}{4}$D．$\frac{2π}{3}$
6．设函数f（x）=sin2x+a（1+cosx）-2x在x=$\frac{5π}{6}$处取得极值．
（1）若f（x）的导函数为f'（x），求f'（x）的最值；
（2）当x∈[0，π]时，求f（x）的最值．
3．已知等差数列{an}的前n项和为Sn，a2=0，S5=2a4-1．
（1）求数列{an}的通项公式；
（2）设bn=2${\;}^{{a}_{n}}$，求数列{bn}的前n项和Tn．
4．已知函数y=tanωx在区间（0，$\frac{π}{4}$），（$\frac{π}{4}，\frac{π}{2}$）上单调递增，但在区间（0，$\frac{π}{2}$）上没有单调性，则ω可以是（　　）
A．-2B．2C．-1D．1

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网