题目内容
1.已知不等式xy≤ax2+2y2,若对任意x∈(1,2),且y∈[2,3],该不等式恒成立,其实数a的取值范围.分析 由已知不等式分离参数a,得到a≥$-2(\frac{y}{x}-\frac{1}{4})^{2}+\frac{1}{8}$,在坐标平面内画出不等式组$\left\{\begin{array}{l}{1<x<2}\\{2≤y≤3}\end{array}\right.$表示的平面区域,求出$\frac{y}{x}$的取值范围,则答案可求.
解答 解:依题意得,当x∈(1,2)时,且y∈[2,3]时,不等式xy≤ax2+2y2,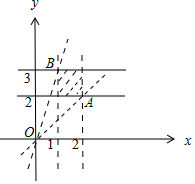
即$a≥\frac{{xy-2{y^2}}}{x^2}=\frac{y}{x}-2•{({\frac{y}{x}})^2}=-2{({\frac{y}{x}-\frac{1}{4}})^2}+\frac{1}{8}$.
在坐标平面内画出不等式组$\left\{\begin{array}{l}{1<x<2}\\{2≤y≤3}\end{array}\right.$表示的平面区域,
注意到$\frac{y}{x}$可视为该区域内的点(x,y)与原点连线的斜率,结合图形可知,$\frac{y}{x}$的取值范围是(1,3),
此时$-2{({\frac{y}{x}-\frac{1}{4}})^2}+\frac{1}{8}$<-1,
因此满足题意的实数a的取值范围是a≥-1.
点评 本题考查简单的线性规划,考查数学转化思想方法和数形结合的解题思想方法,是中档题.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
9.已知动直线l平分圆C:(x-2)2+(y-1)2=1,则直线l与圆O:$\left\{\begin{array}{l}x=3cosθ\\ y=3sinθ\end{array}\right.$(θ为参数)的位置关系是( )
| A. | 相交 | B. | 相切 | C. | 相离 | D. | 过圆心 |
13.若方程$\sqrt{3}$sinx-cosx=a在x∈[0,π]上有两个不同的实数解,则实数a的取值范围是( )
| A. | [1,2) | B. | (1,2] | C. | [-1,0] | D. | [0,1] |
11.抛物线y2=2px的准线经过点(-2,0),则该抛物线的焦点坐标为( )
| A. | (-2,0) | B. | (2,0) | C. | (0,-1) | D. | (0,1) |
 的四个等腰三角形,及其底边构成的正方形所组成,该八边形的面积为( )
的四个等腰三角形,及其底边构成的正方形所组成,该八边形的面积为( )
 B.
B.
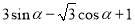 D.
D.