题目内容
18．已知${（1-2x）^6}={a_0}+{a_1}x+{a_2}{x^2}+{a_3}{x^3}+{a_4}{x^4}+{a_5}{x^5}+{a_6}{x^6}$，则|a0|+|a1|+|a2|+|a3|+|a4|+|a5|+|a6|的值为（ ）| A． | 729 | B． | 243 | C． | 64 | D． | 1 |
分析 利用赋值法，x=-1，代入求解即可．
解答 解：${（1-2x）^6}={a_0}+{a_1}x+{a_2}{x^2}+{a_3}{x^3}+{a_4}{x^4}+{a_5}{x^5}+{a_6}{x^6}$，
x=-1时，则|a0|+|a1|+|a2|+|a3|+|a4|+|a5|+|a6|=36=729．
故选：A．
点评 本题考查二项式定理的应用，赋值法的应用，考查计算能力．
练习册系列答案
考前必练系列答案
相关题目
13．
已知正方形ABCD的边长是a，依次连接正方形ABCD的各边中点得到一个新的正方形，再依次连接新正方形的各边中点又得到一个新的正方形，按此规律，依次得到一系列的正方形，如图所示，现有一只小虫从A点出发，沿正方形的边逆时针方向爬行，每遇到新正方形的顶点时，沿这个新正方形的边逆时针方向爬行，如此下去，爬行了10条线段，则这10条线段的长度的和是（ ）
已知正方形ABCD的边长是a，依次连接正方形ABCD的各边中点得到一个新的正方形，再依次连接新正方形的各边中点又得到一个新的正方形，按此规律，依次得到一系列的正方形，如图所示，现有一只小虫从A点出发，沿正方形的边逆时针方向爬行，每遇到新正方形的顶点时，沿这个新正方形的边逆时针方向爬行，如此下去，爬行了10条线段，则这10条线段的长度的和是（ ）| A． | $\frac{31}{128}（2+\sqrt{2}）a$ | B． | $\frac{31}{64}（2+\sqrt{2}）a$ | C． | $（1+\frac{{\sqrt{2}}}{32}）a$ | D． | $（1-\frac{{\sqrt{2}}}{32}）a$ |
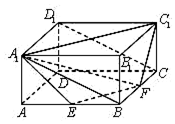如图，在长方体ABCD-A1B1C1D1中，AA1=1，AB=AD=2，E，F分别是棱AB，BC的中点，证明A1，C1，F，E四点共面，并求点B到平面A1EF的距离．