题目内容
下列数列是等差数列的是（ ）
| A、an=-2n |
| B、an=（-1）n•n |
| C、an=（n+1）2 |
| D、an=2n+1 |
考点：等差数列的性质
专题：规律型,等差数列与等比数列
分析：由等差数列的通项公式，可得通项为n的一次函数形式，即可得出结论．
解答：
解：由等差数列的通项公式，可得通项为n的一次函数形式，故可知选A．
故选：A．
故选：A．
点评：本题考查等差数列的通项公式，比较基础．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
曲线y=2x2在点（1，2）处的瞬时变化率为（ ）
| A、2 | B、4 | C、5 | D、6 |
已知数列{xn}满足xn+2=xn+1-xn（n∈N*），x1=1，x2=3，记S=x1+x2+…+xn，则下列结论正确的是（ ）
| A、x100=-1，S100=5 |
| B、x100=-3，S100=5 |
| C、x100=-3，S100=2 |
| D、x100=-1，S100=2 |
若f（x）=sinα-cosx，则f′（α）等于（ ）
| A、sinα |
| B、cosα |
| C、2sinα |
| D、sinα+cosα |
已知sin（α+75°）=
，则cos（α-15°）=（ ）
| 1 |
| 2 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
| 1 |
| i |
| A、1 | B、i | C、-i | D、-1 |
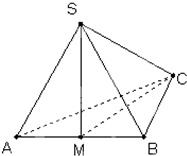如图，在三棱锥S-ABC中，△ABC是边长为4的正三角形，平面SAC⊥平面ABC，SA=SC=2