题目内容
设α∈(π,
),且tanα=
,则sinα= .
| 3π |
| 2 |
| 3 |
| 4 |
考点:同角三角函数基本关系的运用
专题:三角函数的求值
分析:由α的范围及tanα的值,利用同角三角函数间基本关系求出cosα的值,即可确定出sinα的值.
解答:
解:∵α∈(π,
),且tanα=
,
∴cosα=-
=-
,
则sinα=-
=-
.
故答案为:-
| 3π |
| 2 |
| 3 |
| 4 |
∴cosα=-
|
| 4 |
| 5 |
则sinα=-
| 1-cos2α |
| 3 |
| 5 |
故答案为:-
| 3 |
| 5 |
点评:此题考查了同角三角函数基本关系的运用,熟练掌握基本关系是解本题的关键.

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案
相关题目
给出一个算法的程序框图(如图所示),该程序框图的功能是( )
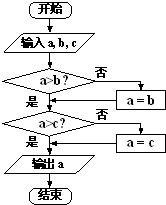

| A、求输出a,b,c三数的最大数 |
| B、求输出a,b,c三数的最小数 |
| C、将a,b,c按从小到大排列 |
| D、将a,b,c按从大到小排列 |
