题目内容
3．函数f（x）=$\frac{1}{2}$x-sinx的大致图象可能是（ ）| A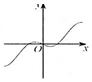． |  | B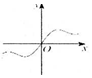． |  | C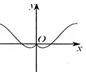． |  | D． |  |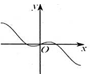
分析 利用函数的奇偶性排除选项，利用导函数求解极值判断即可．
解答 解：函数f（x）=$\frac{1}{2}$x-sinx是奇函数，排除选项C．
f′（x）=$\frac{1}{2}$-cosx，x∈（0，$\frac{π}{3}$），f′（x）＜0函数是减函数，
排除B，D．
故选：A．
点评 本题考查函数的单调性与函数的极值的关系，函数的图象的判断，考查计算能力．
练习册系列答案
优学名师名题系列答案
相关题目
13．若M={x|-2≤x≤2}，N={x|y=log2（x-1）}，则M∩N=（ ）
| A． | {x|-2≤x＜0} | B． | {x|-1＜x＜0} | C． | {-2，0} | D． | {x|1＜x≤2} |
11．下列选项中说法正确的是（ ）
| A． | 命题“p∨q为真”是命题“p∧q为真”的必要条件 | |
| B． | 向量$\overrightarrow{a}$，$\overrightarrow{b}$满足$\overrightarrow{a}•\overrightarrow{b}＞0$，则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为锐角 | |
| C． | 若am2≤bm2，则a≤b | |
| D． | “?x0∈R，x02-x0≤0”的否定是“?x∈R，x2-x≥0” |
15．在区间[0，1]上随机选取两个数x和y，则y＞2x的概率为（ ）
| A． | $\frac{1}{4}$ | B． | $\frac{1}{2}$ | C． | $\frac{3}{4}$ | D． | $\frac{1}{3}$ |
12．
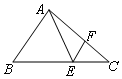如图，在△ABC中，E，F分别是边BC，AC上的点，且△ABE是边长为3的正三角形，EF∥AB，EF=1，则sinC等于（ ）
如图，在△ABC中，E，F分别是边BC，AC上的点，且△ABE是边长为3的正三角形，EF∥AB，EF=1，则sinC等于（ ）| A． | $\frac{{\sqrt{7}}}{14}$ | B． | $\frac{{\sqrt{7}}}{7}$ | C． | $\frac{{\sqrt{21}}}{14}$ | D． | $\frac{{\sqrt{21}}}{7}$ |
13．宿州市日前提出，要提升市民的生活质量，改善民生，促进“中国梦”的实线，为此，某记者在街头随机采访了100名市民，根据他们对“中国梦”实线的信心情况进行统计分析，得到如下分布表：
（Ⅰ）以这100名市民信心指数为样本来估计市民的总体信心指数，若要从全市市民中随机任选3人进行信心跟踪，记ξ表示抽到信心级别为“非常有信心或有信心”市民人数，求ξ的分布列及期望；
（Ⅱ）从这100名市民中，任选两人，记他们的信心指数分别为m、n，求|m-n|≥60的概率．
| 信心级别 | 非常有信心 | 有信心 | 不知道 | 没信心 |
| 信心指数（分数） | 90 | 60 | 30 | 6 |
| 人数（名） | 42 | 38 | 14 | 6 |
（Ⅱ）从这100名市民中，任选两人，记他们的信心指数分别为m、n，求|m-n|≥60的概率．