题目内容
13.若M={x|-2≤x≤2},N={x|y=log2(x-1)},则M∩N=( )| A. | {x|-2≤x<0} | B. | {x|-1<x<0} | C. | {-2,0} | D. | {x|1<x≤2} |
分析 求出N中x的范围确定出N,找出M与N的交集即可.
解答 解:由N中y=log2(x-1),得到x-1>0,
解得:x>1,即N={x|x>1},
∵M={x|-2≤x≤2},
∴M∩N={x|1<x≤2},
故选:D.
点评 此题考查了交集及其运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
1.已知点A是抛物线M:y2=2px(p>0)与圆$C:{x^2}+{(y-2\sqrt{2})^2}={a^2}$在第一象限的公共点,且点A到抛物线M焦点F的距离等于a.若抛物线M上一动点到其准线与到点C的距离之和的最小值为2a,则p为( )
| A. | $\sqrt{2}$ | B. | 2 | C. | $2\sqrt{2}$ | D. | 4 |
18. 已知一个几何体的三视图如右图所示(单位:cm),则该几何体的体积为( )
已知一个几何体的三视图如右图所示(单位:cm),则该几何体的体积为( )
 已知一个几何体的三视图如右图所示(单位:cm),则该几何体的体积为( )
已知一个几何体的三视图如右图所示(单位:cm),则该几何体的体积为( )| A. | 12cm3 | B. | 16cm3 | C. | 18cm3 | D. | 20cm3 |
5.已知非零向量$\overrightarrow a,\overrightarrow b$满足$|{\overrightarrow a+\overrightarrow b}|=|{\overrightarrow a-\overrightarrow b}|=2,|{\overrightarrow a}|=1$,则$\overrightarrow a+\overrightarrow b$与$\overrightarrow a-\overrightarrow b$的夹角为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
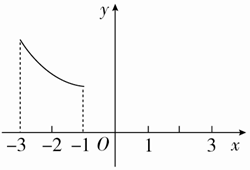 定义在[-3,-1]∪[1,3]上的函数y=f(x)是奇函数,其部分图象如图所示.
定义在[-3,-1]∪[1,3]上的函数y=f(x)是奇函数,其部分图象如图所示.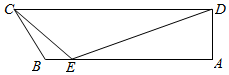 如图,在平面四边形ABCD中,已知∠A=$\frac{π}{2}$,∠B=$\frac{2π}{3}$,AB=6,在AB边上取点E,使得BE=1,连接EC,ED.若∠CED=$\frac{2π}{3}$,EC=$\sqrt{7}$.
如图,在平面四边形ABCD中,已知∠A=$\frac{π}{2}$,∠B=$\frac{2π}{3}$,AB=6,在AB边上取点E,使得BE=1,连接EC,ED.若∠CED=$\frac{2π}{3}$,EC=$\sqrt{7}$.