题目内容
已知f(x)是定义在(-1,1)上的偶函数,且在[0,1)上为增函数,满足f(x-2)-f(4-2x)<0,试确定x的取值范围.
考点:奇偶性与单调性的综合
专题:函数的性质及应用
分析:利用函数的奇偶性和单调性之间的关系将不等式进行转化即可得到结论.
解答:
解:∵知f(x)是定义在(-1,1)上的偶函数,且在[0,1)上为增函数,
∴f(x-2)-f(4-2x)<0等价为f(x-2)<f(4-2x),即f(|x-2|)<f(|4-2x|),
∴
,
即
,
∴
<x<
且x≠2,
故x的取值范围是{x|
<x<
且x≠2}.
∴f(x-2)-f(4-2x)<0等价为f(x-2)<f(4-2x),即f(|x-2|)<f(|4-2x|),
∴
|
即
|
∴
| 3 |
| 2 |
| 5 |
| 2 |
故x的取值范围是{x|
| 3 |
| 2 |
| 5 |
| 2 |
点评:本题主要考查不等式的解法,利用函数的奇偶性和单调性之间的关系将不等式进行转化是解决本题的关键.

练习册系列答案
相关题目
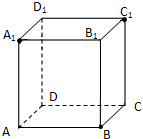 已知正方体ABCD-A1B1C1D1.
已知正方体ABCD-A1B1C1D1.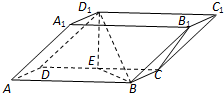 如图,在四棱柱ABCD-A1B1C1D1中,底面ABCD和侧面BCC1B1都是矩形,E是CD的中点,D1E⊥CD,AB=2BC=2.
如图,在四棱柱ABCD-A1B1C1D1中,底面ABCD和侧面BCC1B1都是矩形,E是CD的中点,D1E⊥CD,AB=2BC=2. 小昆和小鹏两人站成一列,背着墙,面朝太阳,小昆靠近墙,在太阳光照射下,小昆的头部影子正好落在墙角处.如果小昆身高为1.6m,离墙距离为3m,小鹏的身高1.5m,离墙的距离为5m,则小鹏的身影是否在小昆的脚下,请通过计算说明
小昆和小鹏两人站成一列,背着墙,面朝太阳,小昆靠近墙,在太阳光照射下,小昆的头部影子正好落在墙角处.如果小昆身高为1.6m,离墙距离为3m,小鹏的身高1.5m,离墙的距离为5m,则小鹏的身影是否在小昆的脚下,请通过计算说明 如图,在直三棱柱ABC-A′B′C′中,AB=AA′=AC=2,∠BAC=
如图,在直三棱柱ABC-A′B′C′中,AB=AA′=AC=2,∠BAC=