题目内容
已知α是第二象限角,sinα=
,函数f(x)=sin2αcosx+cos2αsinx关于直线x=x0对称,则tanx0= .
| 3 |
| 5 |
考点:同角三角函数基本关系的运用
专题:三角函数的求值
分析:由α为第二象限角,根据sinα的值,利用同角三角函数间基本关系求出cosα的值,进而确定出sin2α与cos2α的值,得到cot2α的值,根据函数f(x)=sin2αcosx+cos2αsinx关于直线x=x0对称,确定出x0,代入tanx0,利用诱导公式化简,将cot2α的值代入计算即可求出值.
解答:
解:∵α是第二象限角,sinα=
,
∴cosα=-
=-
,
∴sin2α=2sinαcosα=-
,cos2α=2cos2α-1=
,
∴f(x)=sin2αcosx+cos2αsinx=sin(2α+x)关于直线x=kπ+
对称,
得到2α+x=kπ+
,即x=kπ+
-2α,
则tanx0=tan(kπ+
-2α)=cot2α=
=-
.
故答案为:-
| 3 |
| 5 |
∴cosα=-
| 1-sin2α |
| 4 |
| 5 |
∴sin2α=2sinαcosα=-
| 24 |
| 25 |
| 7 |
| 25 |
∴f(x)=sin2αcosx+cos2αsinx=sin(2α+x)关于直线x=kπ+
| π |
| 2 |
得到2α+x=kπ+
| π |
| 2 |
| π |
| 2 |
则tanx0=tan(kπ+
| π |
| 2 |
| cos2α |
| sin2α |
| 7 |
| 24 |
故答案为:-
| 7 |
| 24 |
点评:此题考查了同角三角基本关系的运用,熟练掌握基本关系是解本题的关键.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
已知方程|2x-1|=a有两个不等实根,则实数a的取值范围是( )
| A、(-∞,0) |
| B、(1,2) |
| C、(0,+∞) |
| D、(0,1) |
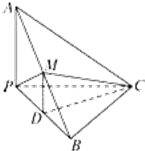 如图,已知三棱锥A-BPC中,AP⊥PC,AC⊥BC,M为AB中点,D为PB中点,且△PMB为正三角形.
如图,已知三棱锥A-BPC中,AP⊥PC,AC⊥BC,M为AB中点,D为PB中点,且△PMB为正三角形.