题目内容
曲线 与直线
与直线 所围成图形的面积为( )
所围成图形的面积为( )
| A.2 | B.1 | C. | D. |
C
解析试题分析:曲线 与直线
与直线 的交点
的交点 ,
,
 曲线
曲线 与直线
与直线 在第一象限围成的面积为
在第一象限围成的面积为 ,
, 围成的总面积为
围成的总面积为
考点:定积分求面积
点评:关键在于正确的求出原函数

练习册系列答案
相关题目
已知 是自然对数底数,若函数
是自然对数底数,若函数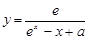 的定义域为
的定义域为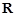 ,则实数
,则实数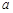 的取值范围为
的取值范围为
A.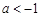 | B.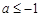 | C.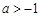 | D.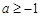 |
定义在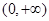 上的可导函数
上的可导函数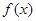 满足:
满足: 且
且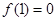 ,则
,则 的解集为( )
的解集为( )
A.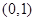 | B.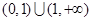 | C.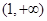 | D.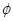 |
函数 的零点所在的一个区间是( ).
的零点所在的一个区间是( ).
| A.(-2,-1) | B.(-1,0) | C.(0,1) | D.(1,2) |
曲线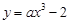 在点
在点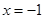 处切线的倾斜角为
处切线的倾斜角为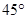 ,那么
,那么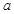 的值为( )
的值为( )
A.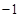 | B. | C.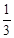 | D. |
由曲线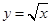 ,直线
,直线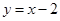 及
及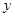 轴所围成的图形的面积为
轴所围成的图形的面积为
A.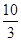 | B.4 | C.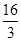 | D.6 |
曲线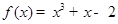 在
在 处的切线平行于直线
处的切线平行于直线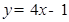 ,则
,则 的坐标为( )
的坐标为( )
| A.( 1 , 0 ) | B.( 2 , 8 ) | C.( 1 , 0 )或(-1, -4) | D.( 2 , 8 )和或(-1, -4) |
设 为实数,函数
为实数,函数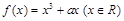 在
在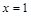 处有极值,则曲线
处有极值,则曲线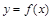 在原点处的切线方程为( )
在原点处的切线方程为( )
A.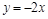 | B. | C.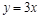 | D. |
 是函数
是函数 的导函数,将
的导函数,将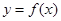 和
和 的图象画在同一个直角坐标系中,不可能正确的是( )
的图象画在同一个直角坐标系中,不可能正确的是( )